CS231n Lecture 3를 듣고 정리한 내용입니다. 발표를 위해 직접 제작한 ppt와 당시 설명했던 내용들을 첨부합니다. 만약 틀린 내용이 있다면 언제든 댓글로 알려주세요! 수정하겠습니다 :)
CS231n Convolutional Neural Networks for Visual Recognition
Table of Contents: Linear Classification In the last section we introduced the problem of Image Classification, which is the task of assigning a single label to an image from a fixed set of categories. Morever, we described the k-Nearest Neighbor (kNN) cla
cs231n.github.io

먼저 지난 시간에 배운 내용을 간단히 복습하겠습니다. Image classification을 할 때 컴퓨터는 그림을 수많은 숫자들로 인식합니다. 그런데 개발자가 직접 이 이미지들을 분류하는 규칙을 만들고 이 물체가 어떤 것인지 판단하려고 하니까 화면에 보이는 예시들과 같은 어려움들이 발생합니다. 같은 object라도 사진이 촬영되는 각도나 빛 등 다양한 조건들에 의해 이렇게나 다양하게 사진이 찍힐 수 있기 때문에, 컴퓨터가 이 모든 것들이 같은 object(고양이)라는 것을 구분하기 어렵습니다. 이런 모든 이미지들에 대해 하나 하나 규칙을 모두 설정해야 한다는 어려움을 극복하기 위해 나온 방안이
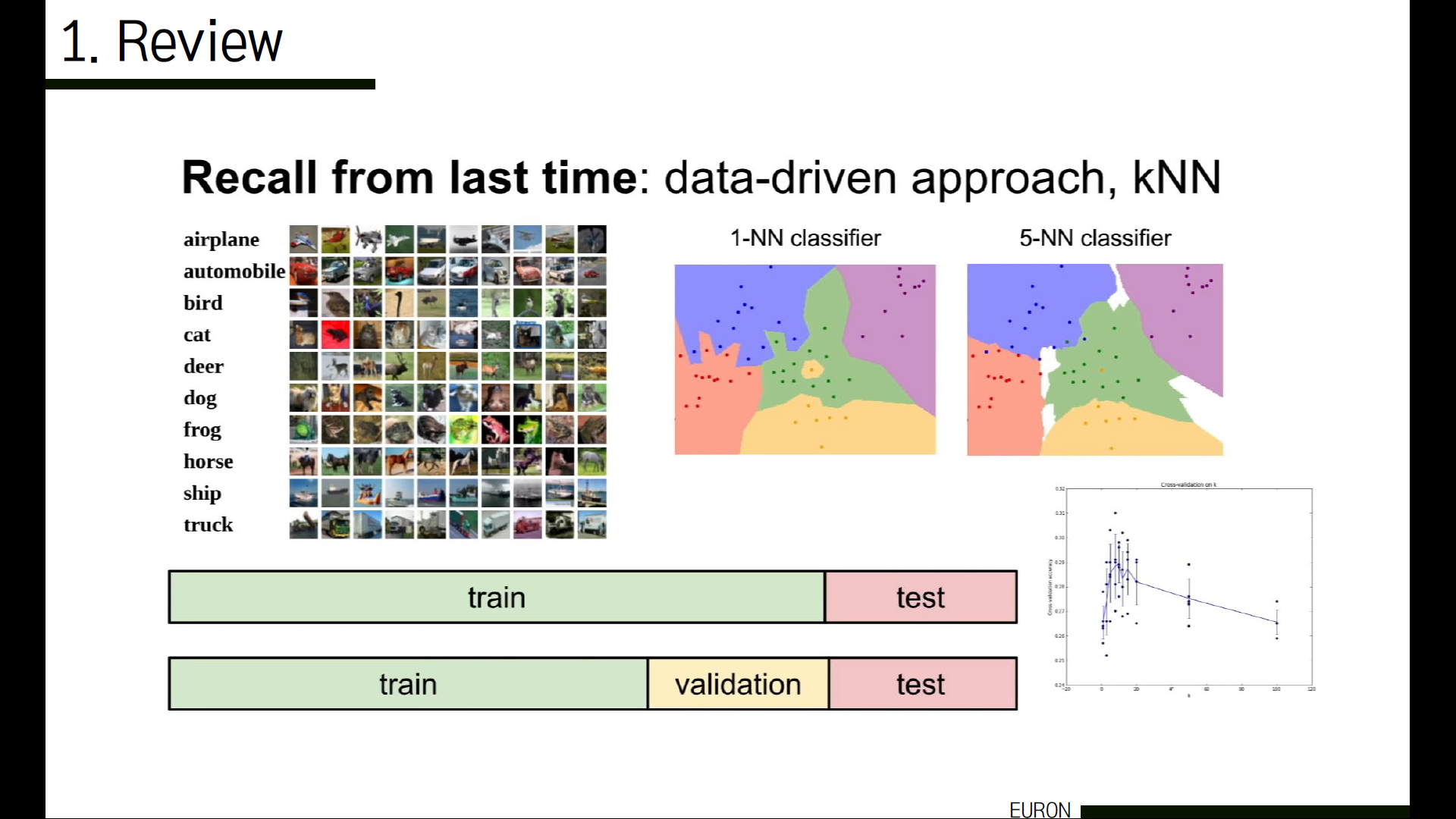
Data-Driven Approaches입니다. 인터넷에서 매우 많은 양의 데이터셋을 모아서 > 데이터들을 학습을 통해 구분하고 정리해서 이러한 이미지 카테고리를 인식 및 분류하는 지식을 요약한 ‘모델’을 만들고 > 이 모델을 사용해 새로운 이미지를 인식하는 방법입니다. 이미지 input이 다양하게 주어지기 때문에 안정성과 확장성이 좋아진다는 장점이 있습니다.
그 다음 살펴볼 내용은 kNN입니다. Nearest Neighbor은 학습된 이미지를 모두 기억하고, 새로운 이미지를 받아서 학습된 데이터들 중 가장 비슷한 이미지를 찾는 방식인데요. 그 중 kNN은 새로운 데이터가 주어졌을 때 기존 데이터 중 가장 가까운 k개 이웃의 정보를 기반으로 새로운 데이터를 예측하는 방법을 말합니다. 저번 시간에 살펴봤던 예시로는 한 가운데 노란 영역에 해당하는 데이터가 있다는 것이었죠. K=1일 때는 컴퓨터는 이 데이터를 노란색 영역에 해당하는 데이터로 분류할 거예요. 하지만 직관적으로 봤을 때 저 부분에 해당하는 데이터는 초록색일 가능성이 더 높지 않을까요? 그래서 K=5로 수정하니 저 데이터를 초록색 영역에 해당하는 데이터로 분류하는 모습을 볼 수 있습니다. 주변 5개의 데이터를 참고해서 결정하다보니 초록색이 될 수밖에 없겠죠.
이렇게 사용자는 여러 번 알고리즘을 수행하면서 최적의 K값을 찾습니다. 이것을 hyperparameters라고 합니다. 하이퍼 파라미터란, 모델에서 외적인 요소로, 데이터 분석을 통해 얻어지는 값이 아니라 사용자가 직접 정하는 값입니다. 가장 좋은 k값이 무엇인지, 어떤 distance를 사용하는 것이 좋은지 등이 이것에 속합니다. 이러한 하이퍼 파라미터를 세팅하는 방법에는 cross-validation이 있습니다. 모든 데이터를 활용해서 특정 데이터에 overfitting되는 것을 방지하고, 정확도를 향상시키기 위해 사용하는 방법입니다. K-fold cross-validation의 경우 K개의 fold로 데이터를 분류한 후 각각 한 fold의 데이터를 validation set으로 활용해 총 K번 검증하고 평균을 내는 방법으로, 모델의 성능을 전체적으로 볼 수 있습니다. 이 방법은 데이터셋이 작을 경우에 사용합니다.
이외에도 임의의 잡음 등을 training set에 가해서 Training set과 현실의 test set 사이의 괴리감을 줄이는 방법으로는 augmentation(flip, noise, contrast, combination 등)에 대해 다뤘습니다. 하지만 kNN은 사실 image에 사용되지 않습니다. 테스트 시간이 매우 오래 걸리고, 이미지의 dimension이 높아질수록 데이터가 많이 필요하기 때문입니다.
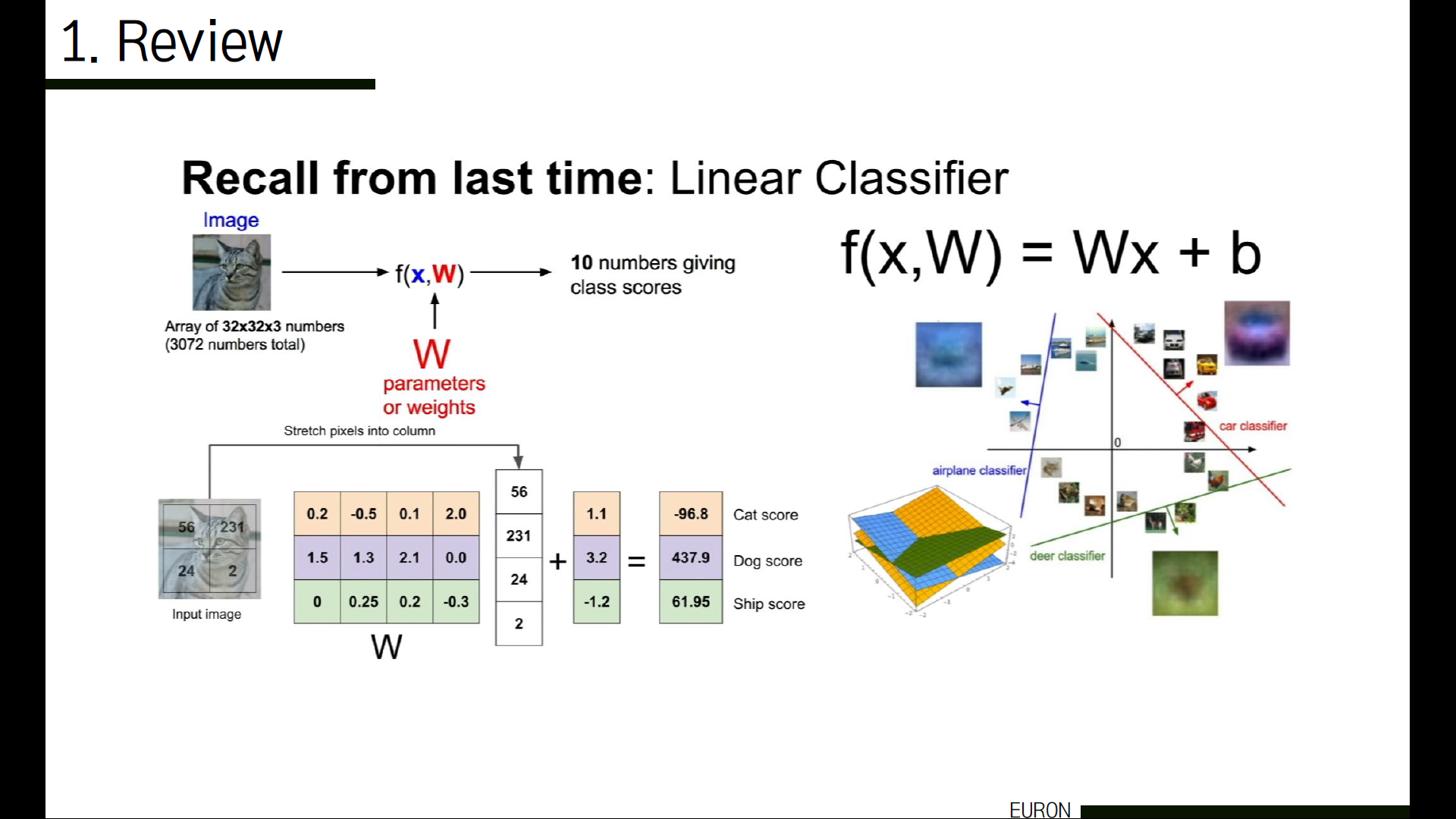
linear classifier(선형 분류)입니다. W는 training data에 대한 정보가 요약된 벡터입니다. kNN에서는 파라미터가 없고 전체 학습된 데이터를 테스트에 사용했던 것과 다르게, 이러한 파라미터들에 학습된 데이터들에 대한 정보가 요약된 벡터를 사용하게 되면서 테스트시마다 전체 데이터셋을 사용할 필요 없이 이 W만 사용해 계산할 수 있게 되었습니다. 따라서 W를 이용해 인풋으로 들어온 이미지를 하나의 긴 column vector로 만들어서, 경우에 따라 b(편향)을 더해준 후 각 class에 대한 score가 담긴 벡터로 결과가 나오게 됩니다.
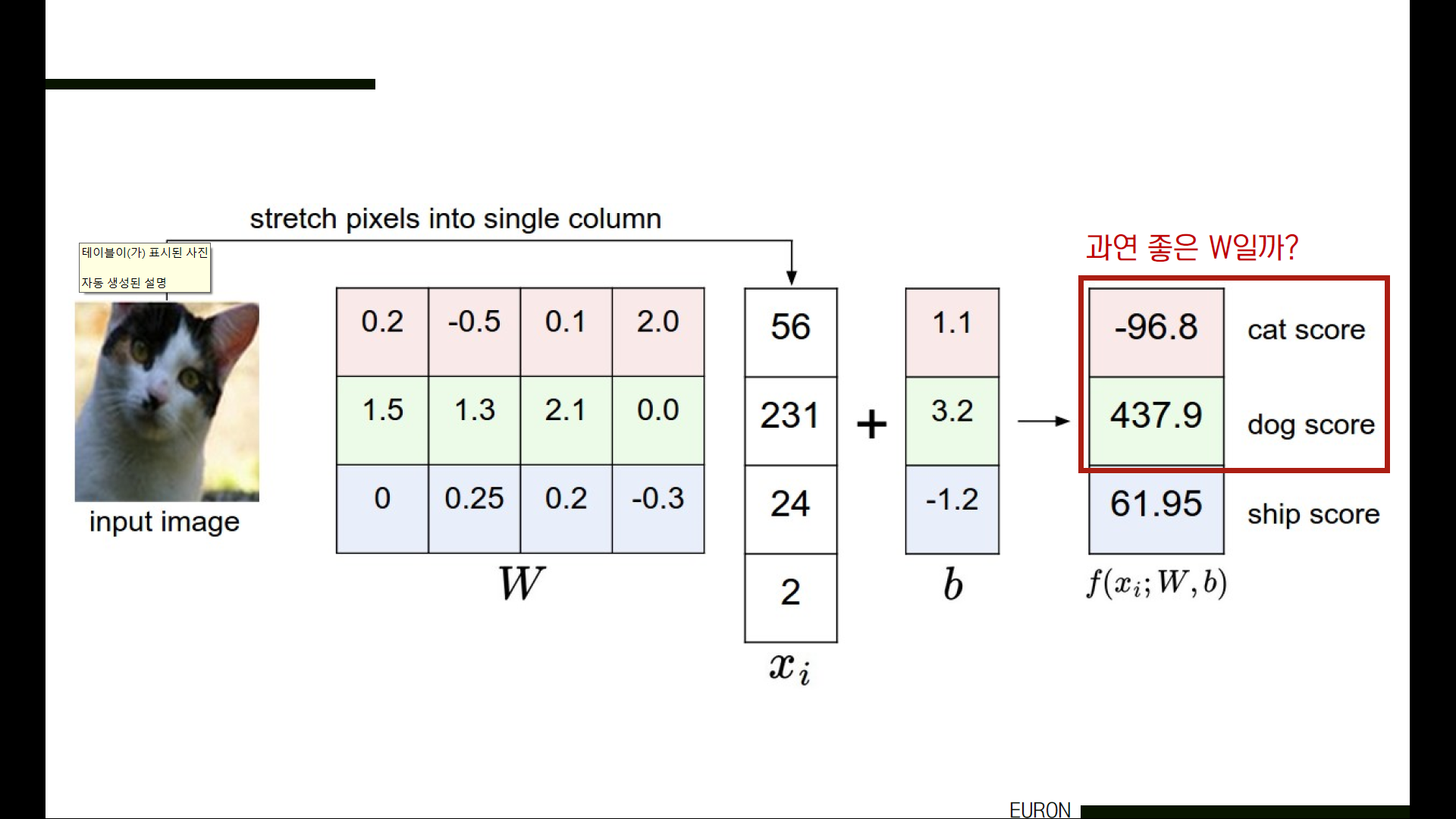
그런데 여기서 고민이 되는 부분은, ‘어떻게 하면 효과적으로 이 W를 선정할 수 있는가?’입니다. 그림을 보시면 고양이 사진을 input으로 주었음에도 불구하고 Dog score가 Cat score에 비해 더 높은 것을 알 수 있습니다. 이것을 좋은 classifier라고 할 수 있을까요? 아니겠죠.

그래서 좋은 W를 선택하기 위한 방법들을 알아야합니다. 이 W를 사용해서 계산했을 때 얼만큼 결과가 좋은지 혹은 나쁜지를 정량적으로 측정해서 판단하는게 필요할 것이고, 만약 결과가 좋지 않다면 좋은 쪽으로 찾아가는 최적화 과정도 필요할 거예요.

바로 이 과정들이 이번 주에 알아볼 loss function과 optimization입니다. 먼저 Loss Function에 대해 알아보겠습니다.

W를 사용해서 계산했을 때 얼만큼 결과가 나쁜가(badness)를 양적으로 측정해서 판단하는 방법입니다. 정말 간단하게 설명을 하자면, 고양이 사진을 넣었을 때 이 classifier가 이 이미지를 고양이라고 분류할 가능성이 제일 높으면 badness가 낮을 것이고, 반대라면 badness가 높을 거예요. 이 badness를 측정하는 방법에는 여러 가지가 있는데요. 우리가 이번 시간에 살펴볼 방법은 Hinge Loss라고도 불리는 Multiclass SVM Loss와, Softmax Classifier입니다.
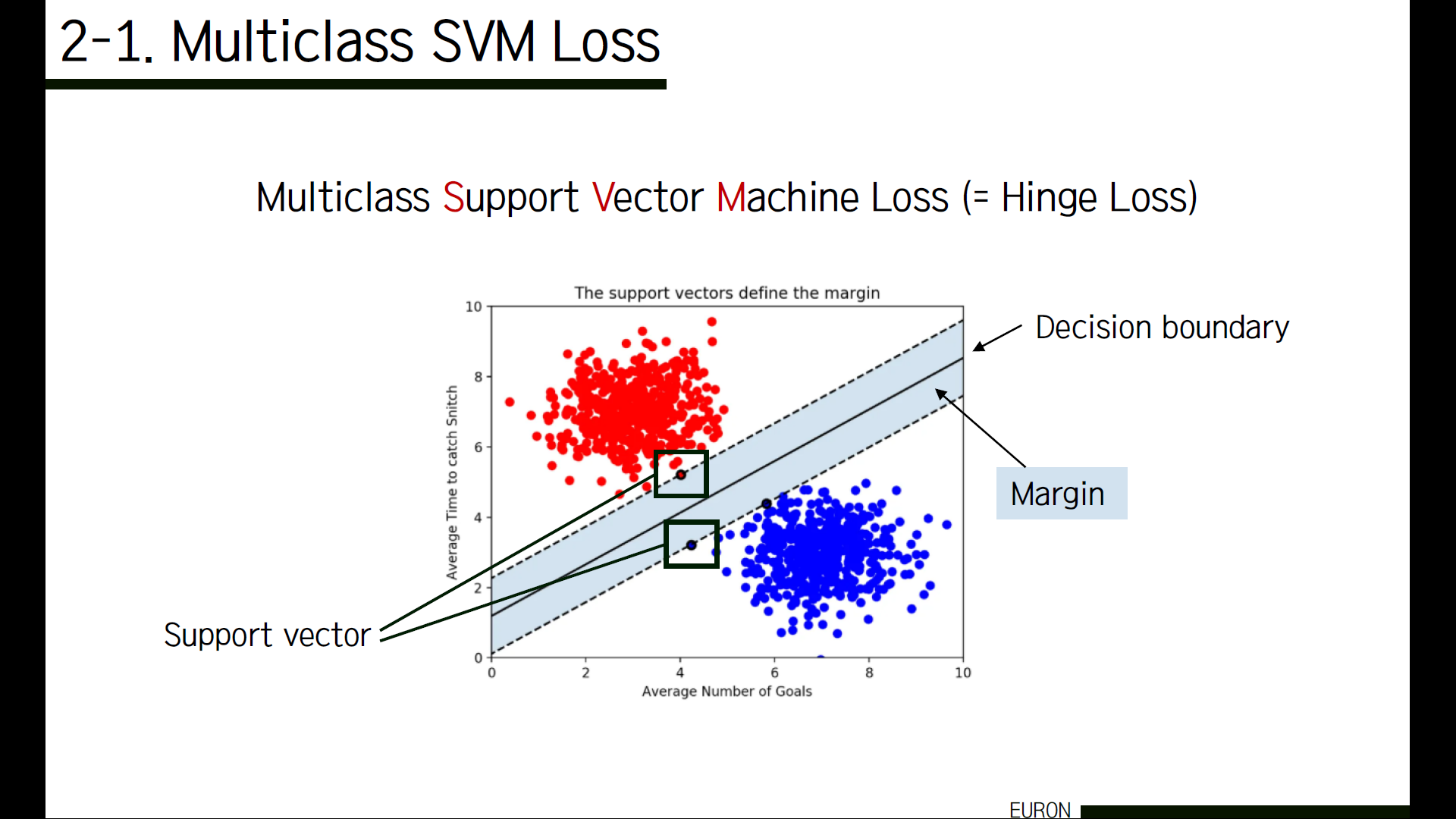
먼저 SVM loss가 무엇인지 알아보겠습니다. SVM은 결국 특정 데이터들을 보다 정확하게 분류하는 것을 목적으로 하는 방법인데요. 위의 그림에서 decision boundary와 가장 가까이 있는 각 그룹별 데이터를 support vector라고 합니다. 이 support vector와 decision boundary 사이의 거리를 margin이라고 합니다. 간단히 말하면, 이 margin을 최대화하는 것이 SVM의 목표라고 할 수 있어요. 우리도 고양이, 자동차, 개구리 등 다양한 class들에 맞게 이미지를 보다 정확하고 뚜렷하게 구분하기 위해 multiclass svm loss를 사용합니다.

Linear classifier를 통과한 이미지는 결과 class 별로 score 값을 가지게 됩니다. SVM loss는 그 이미지에 맞는 정답 클래스의 점수와 오답 클래스의 점수를 비교해서 정답 클래스의 점수가 오답 클래스의 점수보다 크다면 loss가 작아지도록 하는 방법인데요.
왼쪽은 SVM loss의 그래프입니다. 경칩과 같은 모양이라고 해서 SVM loss는 Hinge loss라고도 불립니다. x축은 Syi 값으로 정답 클래스의 score, y축은 loss를 뜻합니다. x값이 커질수록 loss가 0에 가까워지는 것을 볼 수 있습니다. (Sj – Syi +1)의 값이 0보다 작으면 loss의 값은 0이 되고, 그렇지 않으면 이 값은 그대로 loss가 됩니다.
이 식을 말로 정리해보면 Syi(정답 클래스의 점수)가 Sj(정답이 아닌 클래스의 점수) + 마진값보다 클 경우에는 loss가 0이 된다는 뜻이죠. 그런데 이 마진이라는 것이 대체 뭘까요?

예를 들어서, 클래스가 3개 있을 때 정답 클래스의 score가 13이고 나머지 클래스의 score가 각각 -7과 11이라고 해보겠습니다. 마진값이 1일 때는 -7의 경우 max(0, -7-13+1) = 0, 11의 경우 max(0, 11-13+1) = 0입니다. 그런데 마진값을 10으로 잡게 되면 -7의 경우 max(0, -7-13+10) = 0이지만, 11의 경우 13보다 작음에도 불구하고max(0, 11-13+10) = 8인 것을 볼 수 있습니다.
즉 우리가 정한 ‘마진’을 넘어가는 값이 나와야만 loss가 0으로 계산되기 때문에, 마진이 클수록 오답 클래스의 score값에 비해서 정답 클래스의 score값이 매우 차이나게 커야 loss가 작게 나오는 것을 알 수 있습니다. 즉, 정답 클래스에 해당하는 score가 오답 클래스에 해당하는 score보다 ‘마진만큼’ 더 높은 점수를 갖길 원한다는 뜻입니다. 앞으로 보여드리는 예시에서는 마진을 1로 잡아서 계산하도록 하겠습니다.
cf) 왜 마진값을 1로 설정하나요?
사실, 마진이 hyperparameter이기 때문에 cross-validation으로 정하는 것이 정석이긴 하지만 무조건 cross-validation을 실행하지 않아도 마진 값을 1로 설정하면 안전합니다. 왜냐하면 결국 이 score들에 직접적인 영향을 미치는 것은 가중치 W입니다. 그래서 W의 값을 모두 축소하면 점수 차이가 작아지고, W의 값을 모두 확대하면 점수 차이가 커지게 됩니다. 따라서, W 값에 따라 score들의 차이가 변하기 때문에 점수 간 여백(마진)의 정확한 값을 1, 10, 100 등을 정확하게 설정하는 것이 큰 의미를 가지고 있지는 않습니다. 즉, 1로 두어서 정답과 오답 클래스 사이의 score 차이가 일정 부분 더 정확하게 구분지어질 수 있도록 하는데 의의가 있다는 뜻입니다. 따라서 뒤에 나올 예시는 모두 마진값을 1로 설정해 설명합니다.

예를 들어 고양이 사진을 넣어서 cat, car, frog에 해당하는 score가 다음과 같이 나왔다고 해보겠습니다. 각각의 score의 점수에서 cat(올바른 class에 해당하는 score) score를 뺀 후 margin 1을 더해줍니다. 이 결과들을 모두 더하면 이 이미지에 대한 loss입니다. 즉, 고양이 그림에 대해서 2.9만큼 안 좋아!라는 뜻을 가진 수치입니다. 각각의 이미지들에 대한 loss를 구해서 평균을 낸 5.27이 최종 loss입니다.
여기서 만약 저 score들을 살짝씩 바꿔보면 어떻게 될까요? 예시로 Car의 score에서 1을 빼 3.9로 바꿔보겠습니다.

그렇게 해도 loss가 0인 것을 확인할 수 있습니다. 이 경우를 통해 svm loss는 데이터에 민감하지 않다는 것을 알 수 있습니다. SVM loss는 score가 몇점인지에 대해서는 상관하지 않고, 단지 정답 클래스에 해당하는 score가 틀린 class에 해당하는 score보다 높은지만 중요하게 판단합니다.

Q1) 만약 score가 매우 작아져서 모두 0에 가까워지면 어떻게 되나요?
클래스 개수 -1 값이 나오게 됩니다. 이것을 sanity check라고도 부르는데요. 맨 처음 학습 때 가중치는 매우 작게 설정되기 때문에 모든 s 값이 0에 근사하게 됩니다. 이때 loss 값을 계산해보면 각각 미리 설정된 margin만큼 loss가 발생하게 되고, 그것들의 합은 margin * (C-1)가 됩니다. 모든 data에 대해 같은 loss 값이 산출되므로 최종 loss 또한 margin * (C-1)이 되는데, margin은 1이므로 결국 C-1이라는 값을 얻을 수 있습니다. 만약 학습 초기에 sanity check를 해서 결과값이 C-1이 나오지 않는다면 코드에 버그가 있을 수 있기 때문에 확인을 해야합니다. 매우 유용한 디버깅 툴입니다.
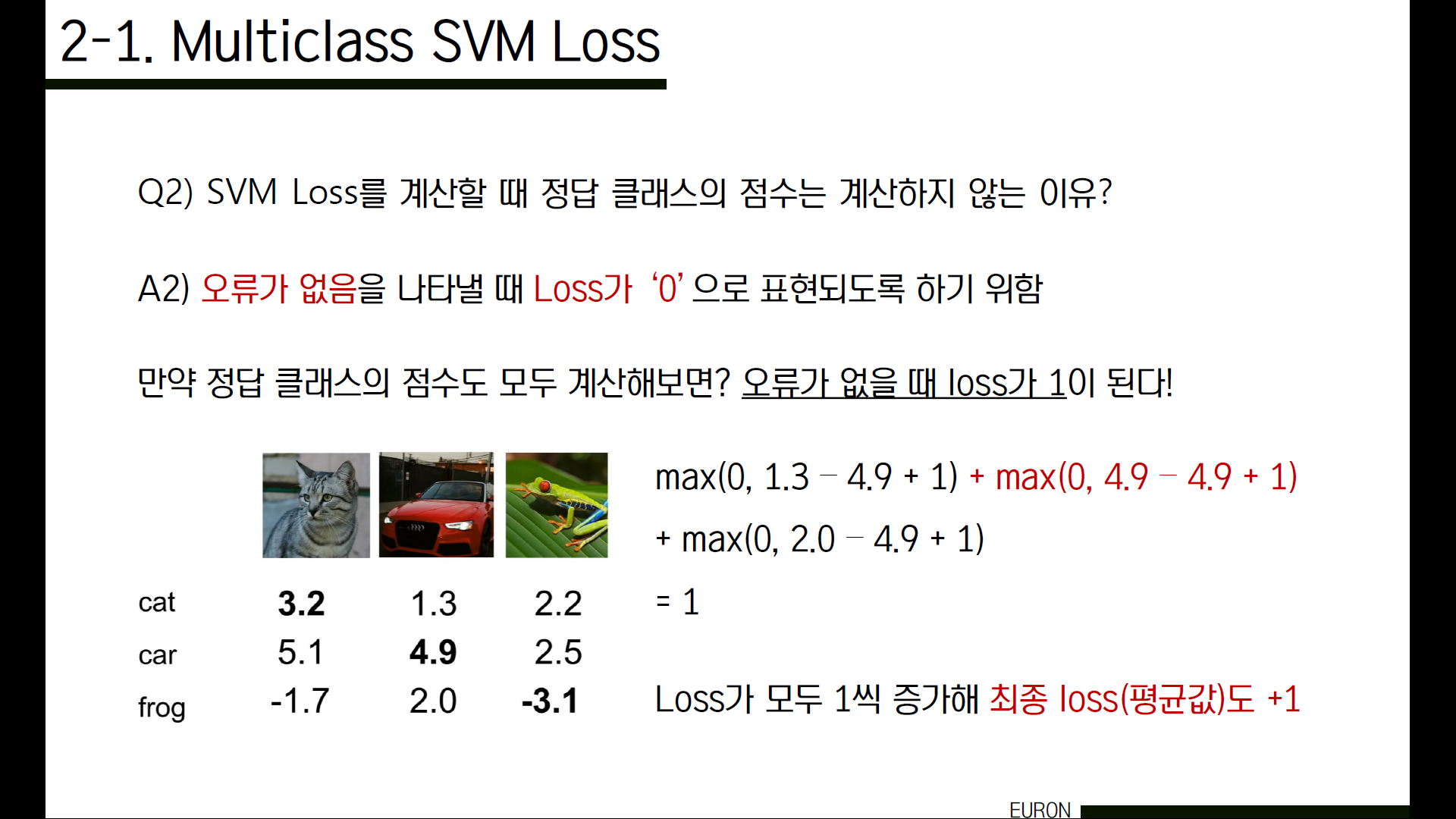
Q2) 이제껏 정답 클래스 score를 제외하고 loss를 구했는데, 왜 정답 클래스는 계산에서 제외한 걸까요?
정답클래스를 포함해서 계산을 해보면 결국 최종 loss값이 +1 되는 것을 알 수 있습니다. 이것은 당연한 결과예요. 왜냐하면 정답 클래스에 해당하는 loss는 Sj와 Syi의 값이 동일하기 때문에 무조건 1이 나오기 때문입니다. 그래서 모든 이미지가 제대로 분류될 경우 최종 loss는 1이 됩니다.
그런데 우리가 구하는 loss는 결국 '얼만큼 나쁜가?'를 의미하는 것이기 때문에 만약 정말 하나도 오류가 없다면 이 loss값이 1인 것보다는 ‘0’으로 표현되는 것이 훨씬 더 직관적이겠죠. loss가 1인데 전혀 나쁘지 않다는 것은 말이 안 되니까요. 그래서 정답클래스를 제외해 계산합니다.

Q3) 만약 식을 이렇게 바꾼다면 값은 어떻게 될까요?
값이 달라집니다. 제곱을 하게 되면 non linear하게 됩니다. 즉, hinge loss 그래프가 직선이 아니라 곡선으로(제곱승으로) 그려지게 됩니다. 그래서 일반적으로는 제곱승을 하지 않고 사용합니다. 이렇게 제곱을 사용하는 squared hinge loss가 별도로 존재하는데요, 어떤 형태가 더 알맞을지는 cross-validation을 통해 결정합니다.

SVM에서는 score의 의미를 이해하는 과정은 필요하지 않았습니다. 정답인 클래스의 score가 틀린 score보다 큰지만 신경썼어요. 이렇게 각 클래스의 score를 사용해 loss를 계산하는 SVM과는 달리, 이번에는 여러 클래스의 score를 일반화해서 직관적인 확률을 따져보겠습니다.
두 번째 loss function인 소프트맥스는, softmax function을 이용합니다. 먼저 구하고자 하는 클래스의 score를 지수화한 값을, 모든 클래스의 score를 지수화해서 더한 값으로 나눠 확률을 구합니다. 이는 기존 클래스들에 해당하는 점수를 합이 1이 되는 정규화된 양수 값으로 바꿔주는 과정으로, 우리가 원하는 class의 정답률이 100% 즉 1에 가까워질수록 loss는 0에 가까워짐을 직관적으로 표현하기 위함입니다.

계산 과정을 보겠습니다. 각 class의 score에 exp를 취합니다. 그 후, 그 값들을 모두 더한 값(188.68)로 각각의 값들을 나눠줍니다. 그렇게 될 경우 확률값이 되겠죠. 마지막으로 우리가 구하고자 하는 정답 클래스(여기서는 고양이)의 확률에 -log를 취해줍니다. 그 결과 0.89가 나왔습니다. 즉, 이 W는 0.89만큼 나쁘다는 뜻입니다. 그런데 왜 결과 값을 -log를 사용해 구할까요?
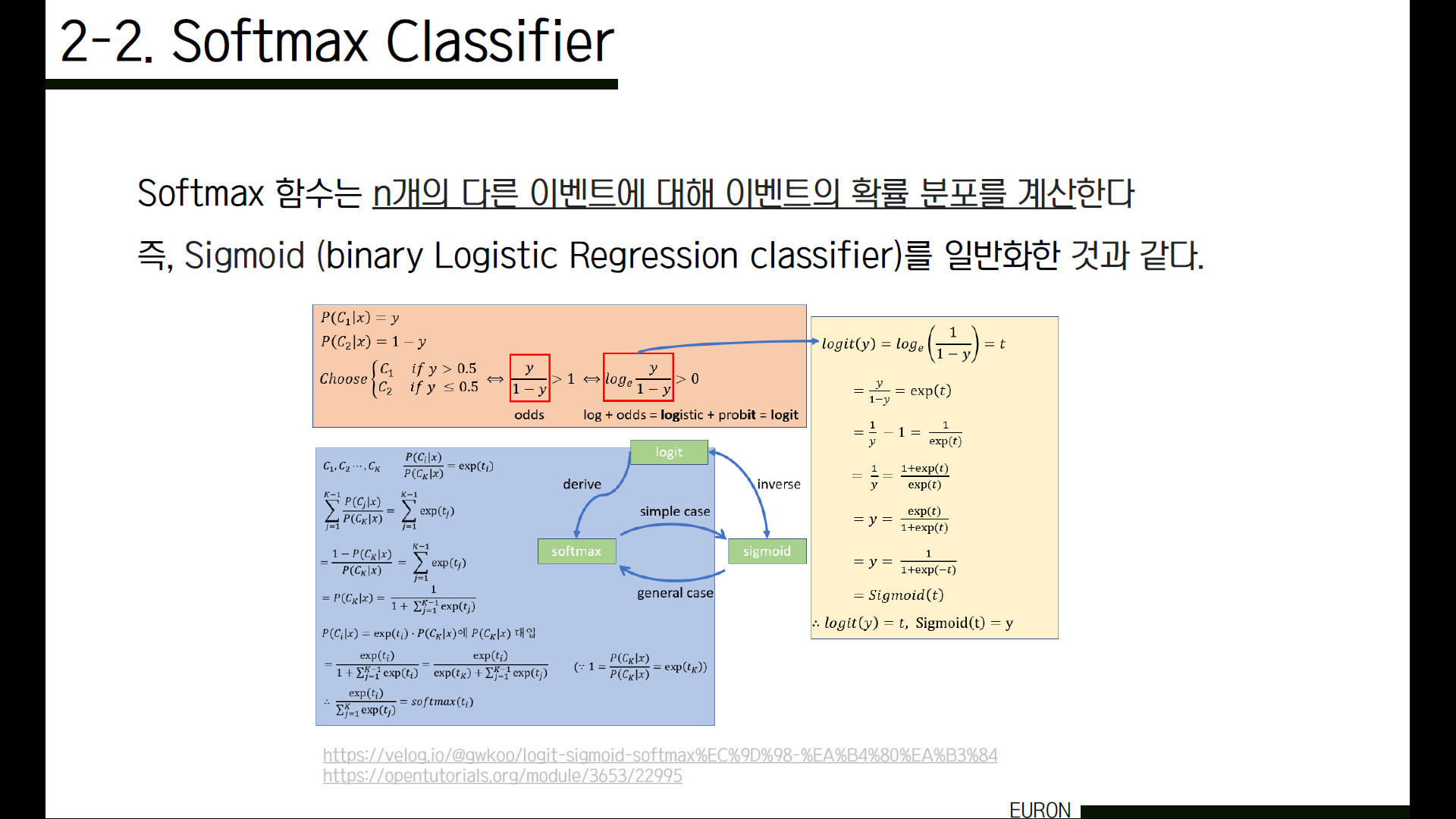
소프트맥스는 n개의 다른 이벤트(여기서는 클래스겠죠)에 대한 확률 분포를 계산하는 멀티노미얼 로지스틱 회귀입니다. 로지스틱 회귀는 sigmoid 함수라고도 불리는데요. 즉, sigmoid 함수를 일반화한 것과 같습니다. 아래 이미지는 sigmoid 함수와 logit, softmax 함수들이 각각 역함수 관계, 일반화해 전개한 함수라는 것을 보여줍니다. 시간상 식 전개를 모두 해볼 수가 없어서, 아래 링크를 남겨두었으니 자세한 수식이 궁금하신 분은 참고하셔도 좋을 것 같습니다.
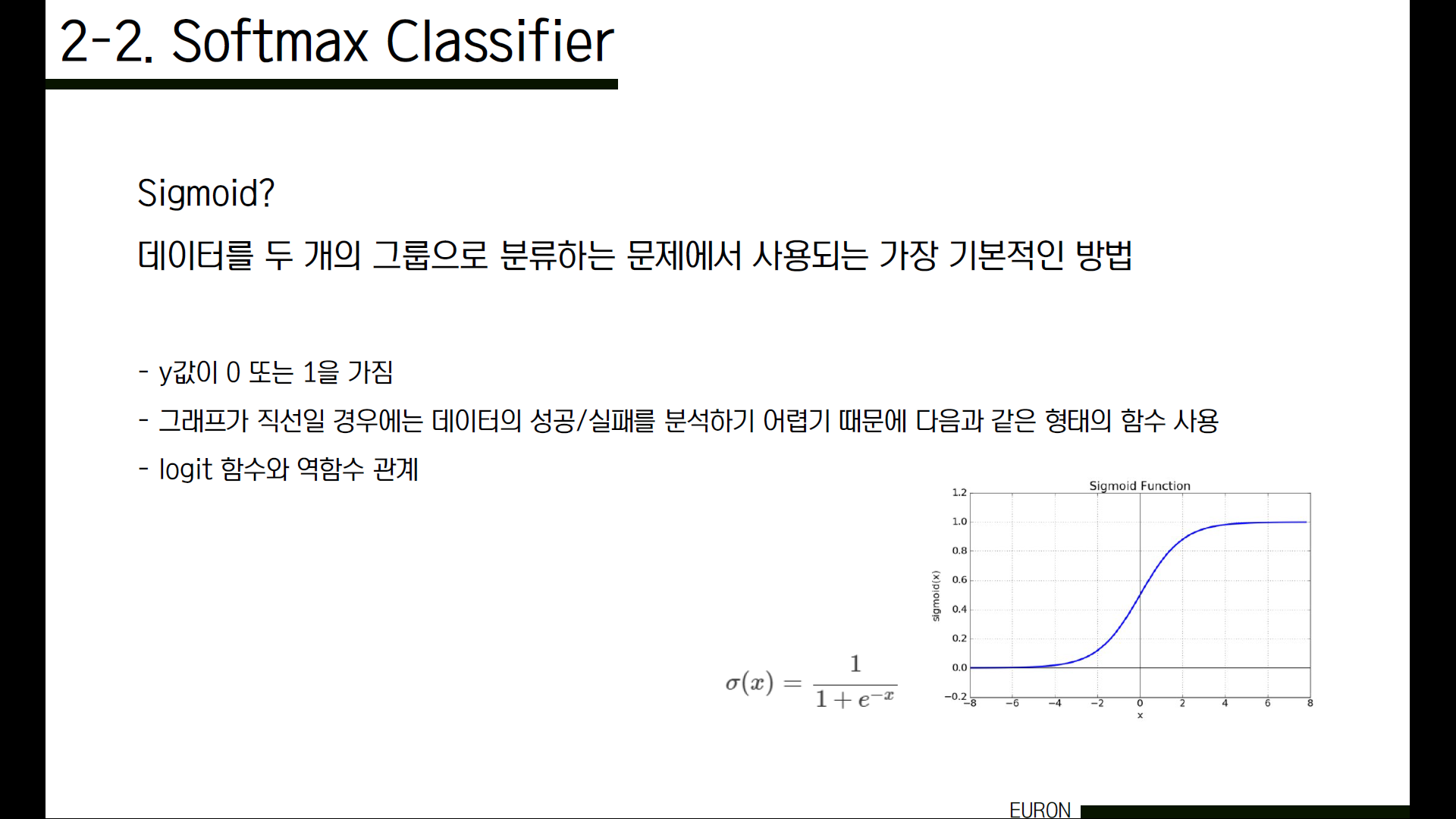
그럼 Sigmoid(시그모이드)란 무엇일까요? 데이터를 두 개의 그룹으로 분류하는 문제에서 가장 기본적인 방법은 로지스틱 회귀분석입니다. 로지스틱 회귀분석에서는 2개의 그룹으로 분류해야 하기 때문에 종속변수 y값이 0 또는 1을 갖습니다. 그런데 그래프가 직선일 경우에는 데이터의 성공과 실패를 분석하기 어렵기 때문에 다음과 같은 형태의 함수를 사용하고 있습니다. 그런데 우리가 사용했던 softmax 함수도 결국엔 확률 분포를 구하는 sigmoid 함수의 일반형이었기 때문에 결과값이 0과 1 사이의 값이었죠.
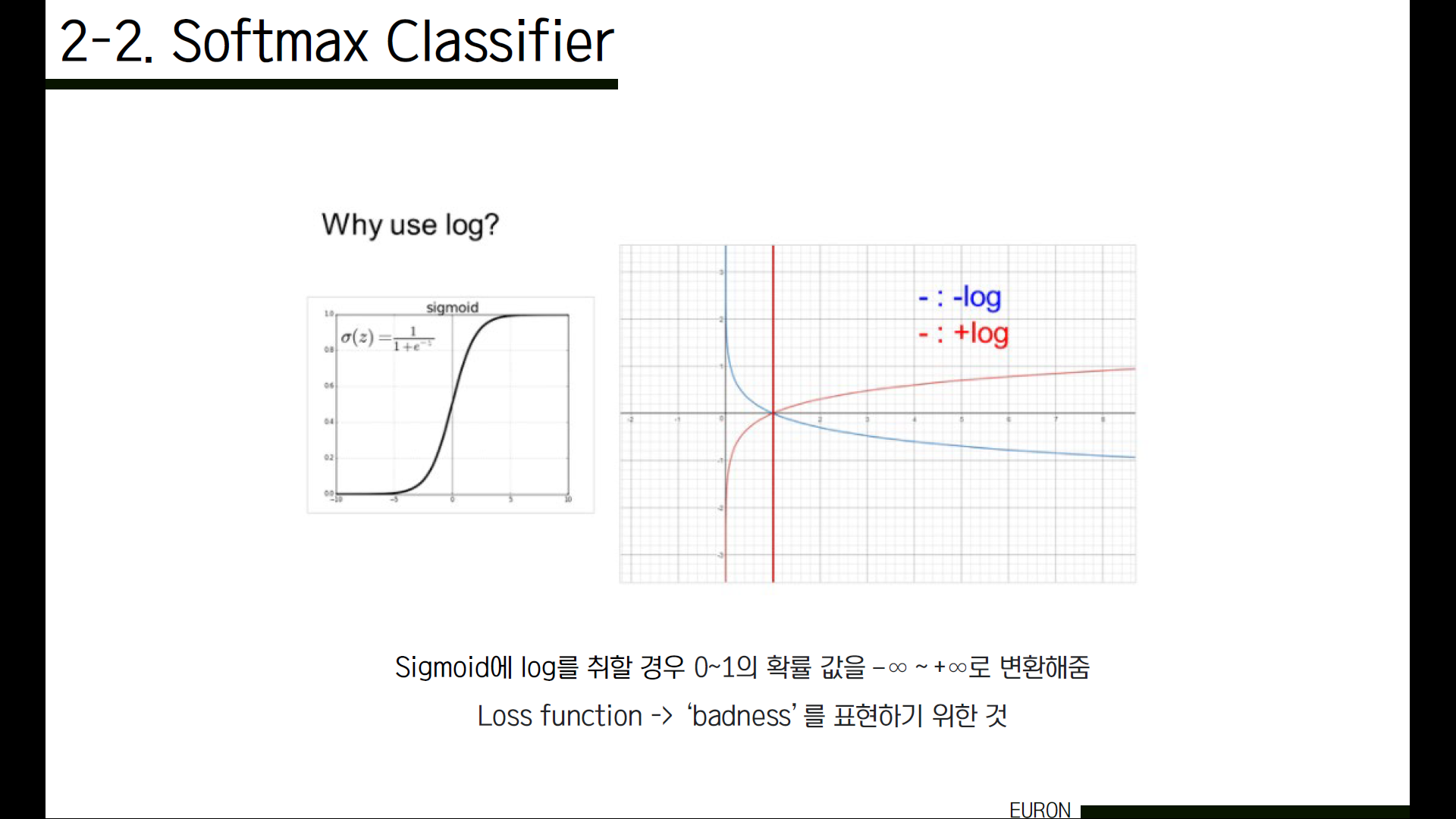
이러한 형태의 함수에 log를 취하게 되면 0에서 1사이의 결과 값, 즉 확률값을 −∞ ~ +∞로 변환해줍니다. 그렇다면, 확률값에 log를 취해 정량적인 badness를 측정하려는 건 알겠는데, 그럼 왜 하필 마이너스 로그를 사용하는 걸까요?
이 그래프에서 x축이 확률, y축이 loss라고 할 때, 우리가 원하는 class의 정답률, 즉 x가 1에 가까우면 100%라는 것이니 x가 1이 될수록 점점 loss는 0에 가까워져야겠죠. 위에서 보여드린 지수화해서 확률을 구하는 방식에서 저 P는 결국 ‘정답을 맞출 확률’입니다. 그런데 Loss function은 결국 ‘얼마나 안좋은지’를 판단하는 것입니다. 그렇다면 ‘정답을 맞출 확률’이 1이 될수록 좋은 것이라면, 이러한 badness를 나타내는 지표는 ‘정답을 맞출 확률’의 음수가 되어야 할 거예요. (즉, x가 1이 될수록 loss 값은 점점 줄어들어야 합니다.) 따라서 정답 클래스가 될 가능성에 minus log를 취한 것이 loss function이 됩니다. 이 badness를 정확하게 표현하기 위해서 우리는 -log를 사용합니다.

Q1) 마찬가지로 score들이 매우 작아져서 0에 가까워지면 어떻게 될까요?
계산해보면 결국 e^0의 값은 1이기 때문에 -log(1/클래스 개수)가 됩니다. 이 방법도 SVM loss와 마찬가지로 디버그 용도로 사용합니다.

Cf) 왜 이론적으로인가?
그래프상 x(0~1)에 대해 y의 치역이 0~무한대인 것은 맞지만 이 값이 나오기 위해서는 x값(각 클래스의 score에 exp를 취한 값)이 0또는 1이 나오는 경우인데 이렇게 되기 위해서는 기존 score의 값이 무한대 혹은 마이너스 무한대여야 합니다. 이러한 경우는 발생하지 않습니다. (컴퓨터가 계산하기 어렵기 때문에 지양해야 합니다.)
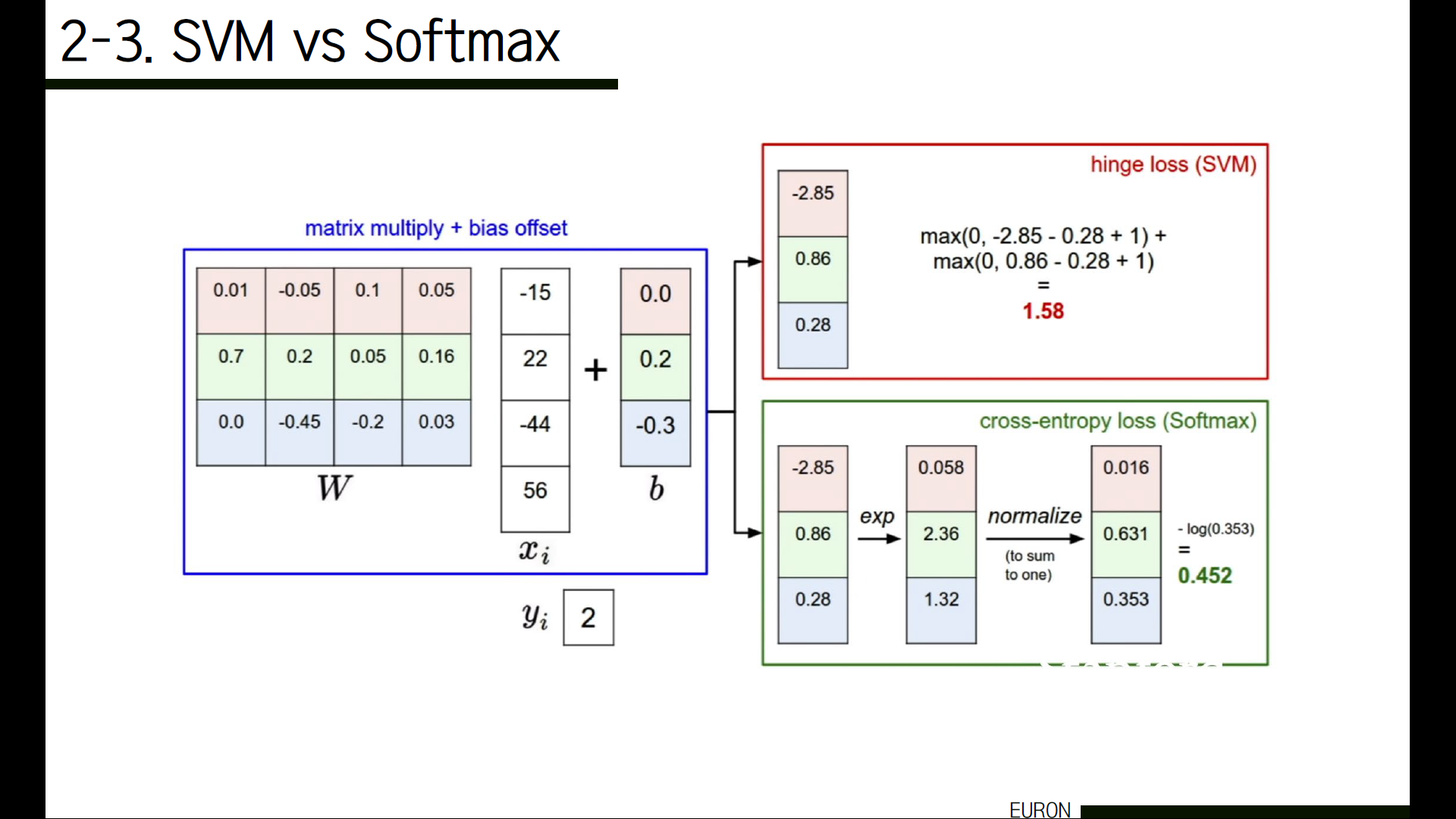
앞서 소개한 두 가지 방식은 모두 동일하게 가중치를 곱한 클래스들의 score를 사용해 badness를 정량적으로 측정하는 방법이라는 공통점이 있는데요. 차이점은 무엇일까요?
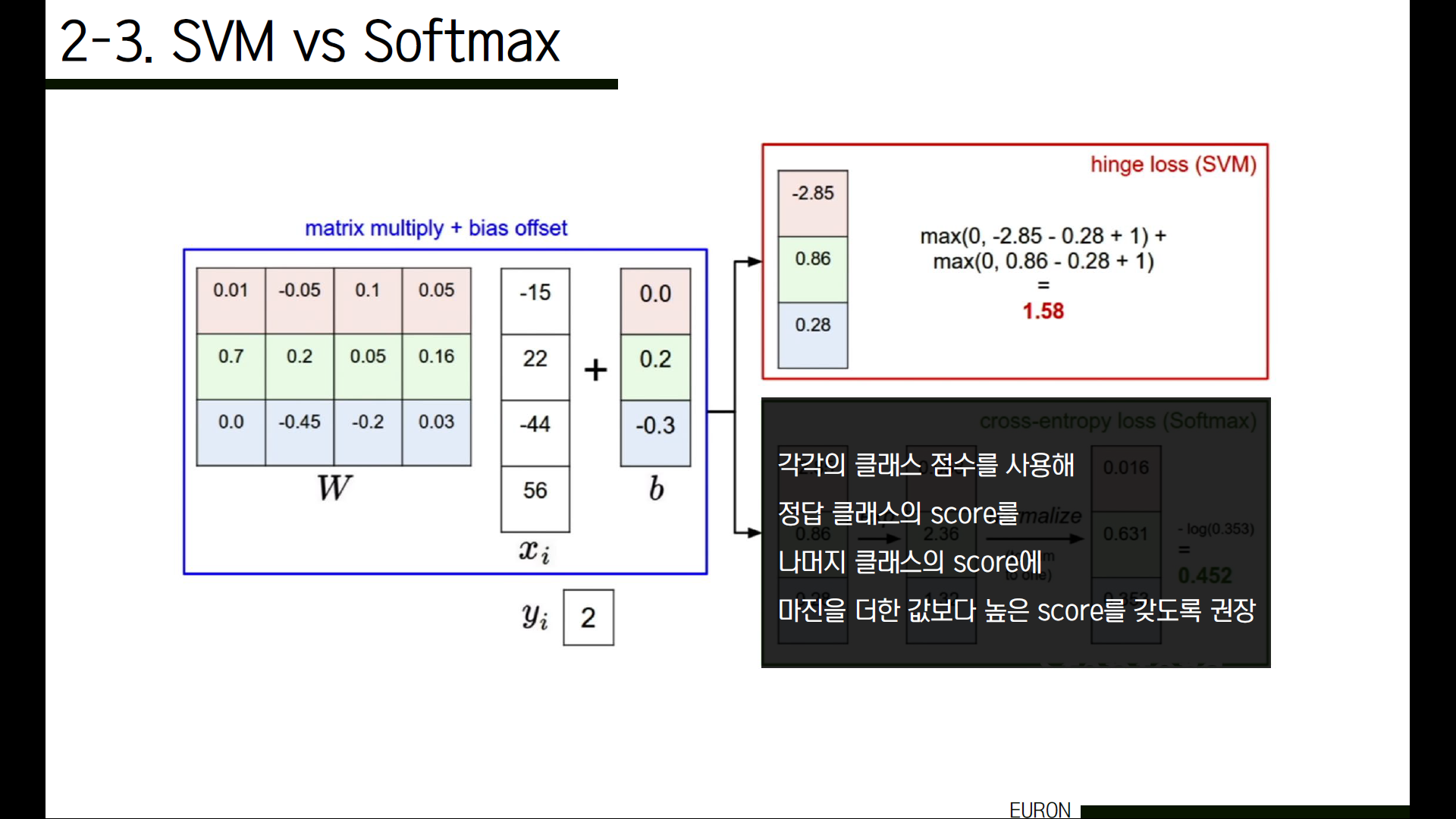
그 차이는 바로 점수 해석에 있습니다. SVM의 경우 각각의 클래스 score를 사용해 정답 클래스의 score가 나머지 클래스의 score에 마진을 더한 값보다 높은 score를 갖도록 권장합니다.
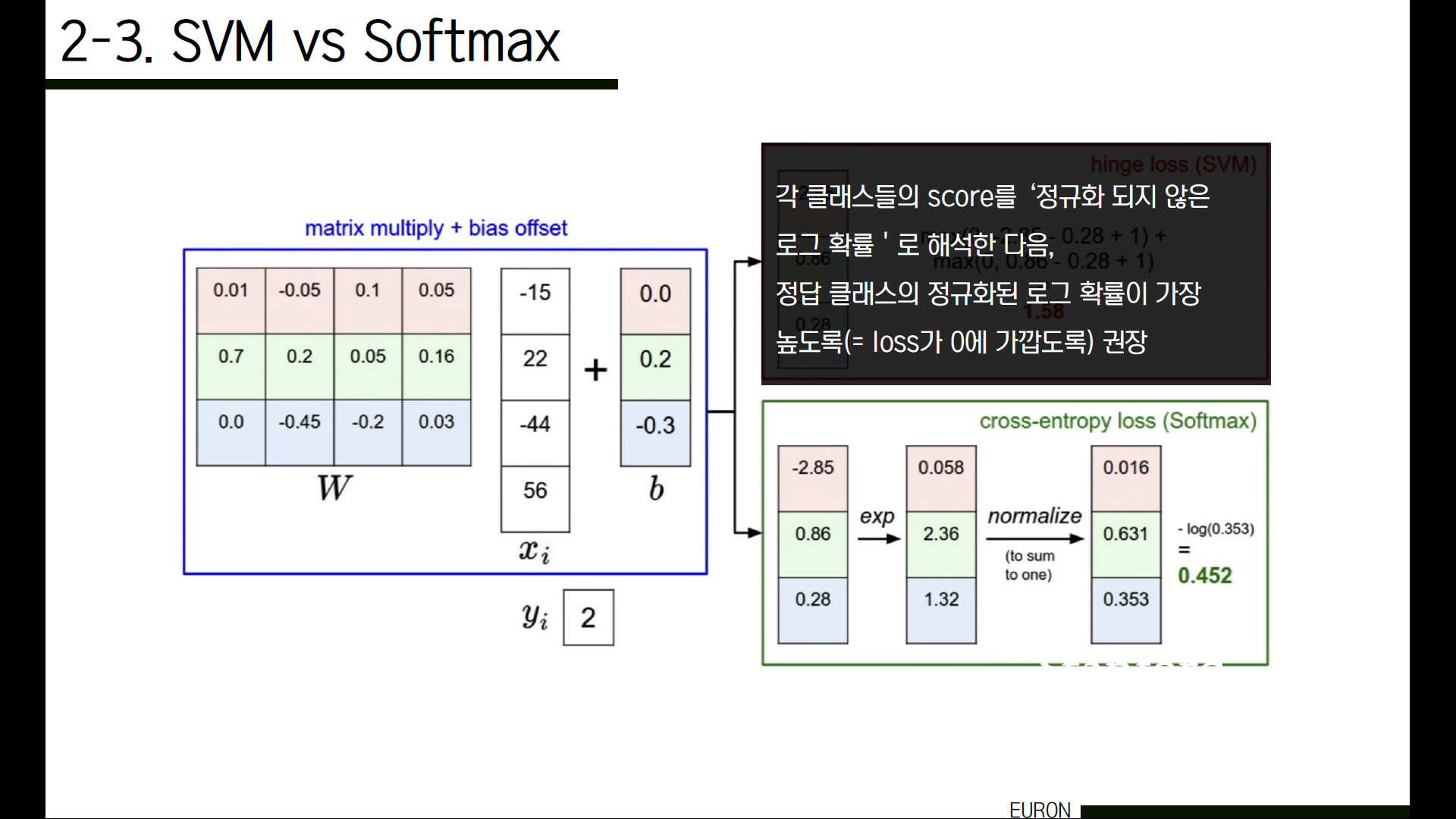
반면에 softmax의 경우에는 이 클래스의 score들을 ‘정규화되지 않은 로그 확률’로 해석한 다음, 정답 클래스의 정규화된 로그 확률이 가장 높도록(즉 loss가 0에 가깝도록) 권장합니다. 정량적으로 이 두 값을 비교하는 것은 의미가 없고, loss를 비교하고 싶다면 같은 loss function을 사용한 것들끼리 비교해야 합니다.

만약 score값을 조금씩 바꿔보면 어떻게 될까요? 앞서 SVM에서 car의 점수를 바꿨을 때는 loss 값에 변동이 없었습니다. 왜냐하면 SVM loss는 정답 클래스의 점수가 정답이 아닌 클래스의 점수 +1 보다만 큰지에 대해서만 신경썼기 때문이에요. 즉, 데이터에 둔감합니다. 하지만 Softmax의 경우 확률로 계산되기 때문에 조금만 데이터가 변경되어도 바로 결과값이 달라지게 됩니다. 데이터에 매우 민감하죠!
즉, softmax classifier는 각 클래스에 대한 확률을 알려줍니다. 각각의 클래스에 대한 점수를 해석하지 않는 SVM과는 달리, softmax의 경우 클래스의 확률을 계산해서 각 클래스의 신뢰도를 해석할 수 있습니다. 하지만 이 확률 또한 정규화 강도(람다)에 따라 달라지기 때문에 절대적인 숫자로 해석해서는 안됩니다.

그런데, 이렇게 우리가 구하는 W가 과연 유일한 값일까요? 유일하지 않다는 것을 바로 확인해볼 수 있습니다. W에 2배, 3배를 해보면 loss가 같은 값이 나옵니다. 즉, W는 여러 개가 될 수 있습니다.
그렇다면 ‘가장 적절한 가중치’를 선택하는 것이 중요한 문제가 되는 이유는 무엇일까요? 결국 우리가 badness를 검증하면서까지 더 좋은 W를 찾아 model을 만드려고 하는 이유는 새로운 값에 대해서 정확하게 예측하고 싶기 때문입니다. 즉, training data가 아닌 test data에 대한 classifier의 퍼포먼스를 고려해야 합니다. Training data에만 맞게 신경쓴다면 실제 데이터를 만났을 때 이상한 결과를 낼 수 있거든요.
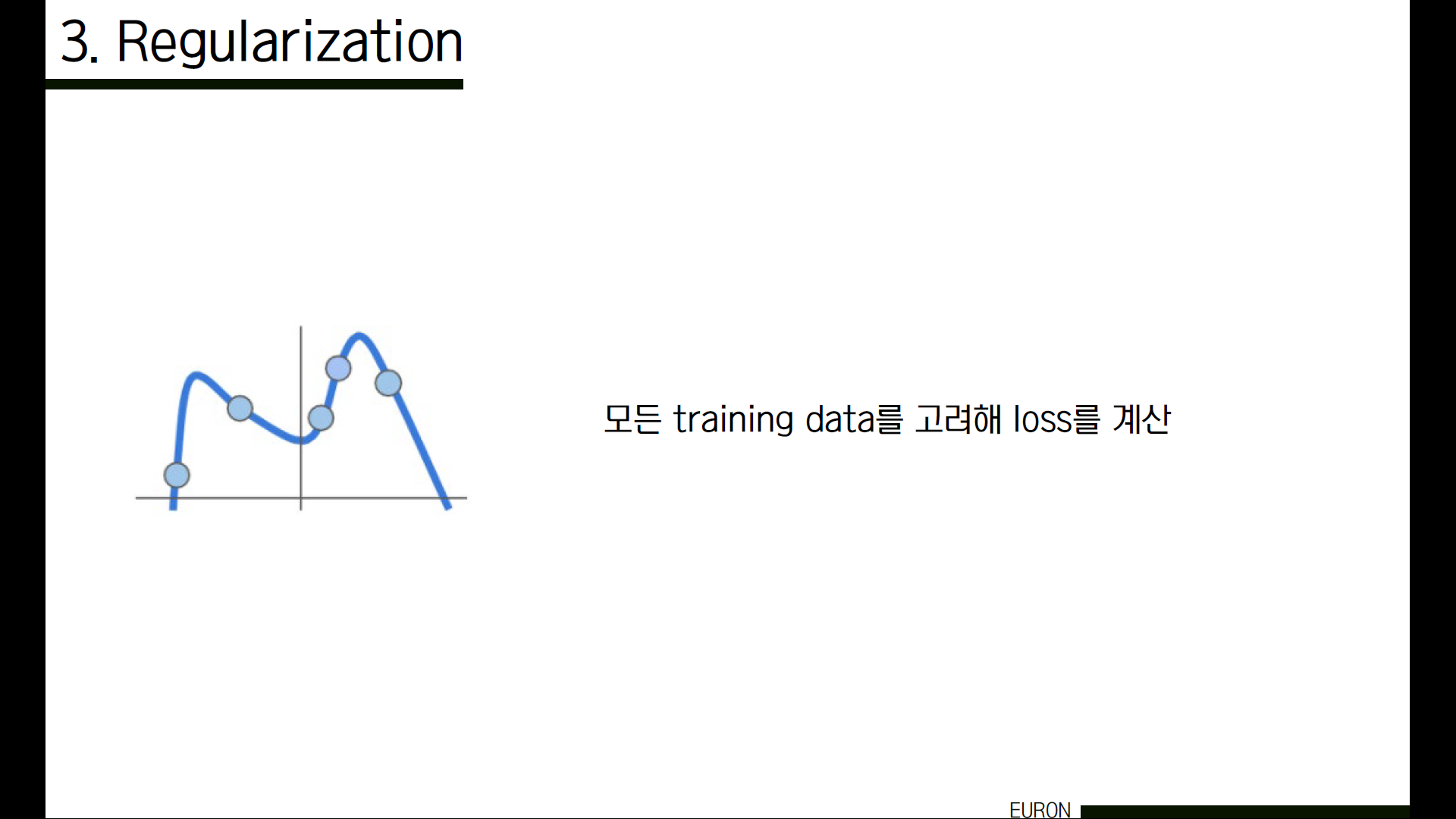
기존 데이터(점)들을 ‘모두’ 고려해서 loss를 계산했다고 해보겠습니다. 그럼 이런 모양의 그래프가 그려질 수 있겠죠.

그런데 test data가 초록색 점들이라면, 이 모델은 초록색 값들이 무엇인지 예측할 수 있을까요? 그래프를 보면 알 수 있듯이 예측 못하거나, 예측한다고 하더라도 굉장히 정확도가 낮을 거예요. 이것을 overfitting(과적합)이라고 합니다.

차라리 training data들을 덜 고려하고 이렇게 단순한 그래프를 그리는 것이 test data를 예측하기 더 쉬울 수 있을 거예요. 이처럼 test data에도 맞는 W값을 찾기 위해 사용하는 것이 바로 정규화입니다.

즉 정규화는 기존 데이터들에만 맞게 학습하려고 할 때 패널티를 주면서 Test data에도 맞는 모델이 될 수 있도록 모델을 더 단순하게 만드는 W를 선택하게 합니다. 더 자세하게 알아보자면, Loss function은 2 가지의 loss를 포함하고 있습니다. 하나는 data loss, 또 하나는 regularization loss입니다. Data loss는 우리가 앞서 여러가지 training data로 loss를 계산했듯이 ‘학습’에 집중하는 것이고, regularization은 기존 데이터들에만 맞게 학습하려고 할 때 패널티를 주면서 test data, 즉 실제로 만나게 될 데이터들에도 맞는 model이 될 수 있도록 model을 더 단순하게 만드는 W를 선택하게 합니다. 이 두 가지를 조절하면서 최적의 W를 찾아가는 거죠. (더 단순한 모델을 찾으려고 하는 것은, 설명이 단순할수록 새로운 것을 예측하는데 더 일반적이기 때문에 가설 중에서 가장 단순한 것을 고르는 것이 좋다는 Occam’s Razor의 아이디어를 참고해보면 이해할 수 있습니다.)
조절은 hyperparameter인 람다 값으로 합니다. 람다는 규제의 강도 값이라고 할 수 있는데요, data loss와 regularization loss를 참고해 값을 변경합니다. 람다 값이 클수록 regularizaion loss가 커지기 때문에 모델이 단순해지고, 작을수록 모델은 복잡해집니다. 따라서 이 값을 너무 과하게 조절할 경우 underfitting/overfitting의 위험이 존재하기 때문에 적절한 값을 설정해 주어야 합니다. (주로 cross-validation 과정을 통해 람다를 결정하게 됩니다.)

가장 많이 쓰이는 정규화 방식으로는 L1규제와 L2 규제가 있습니다. 왜 L1규제에서 feature selection이 더 잘 되는지 이유가 궁금하시다면 수식에 대해 더 찾아보는 것을 권장드립니다. (시간상 생략)
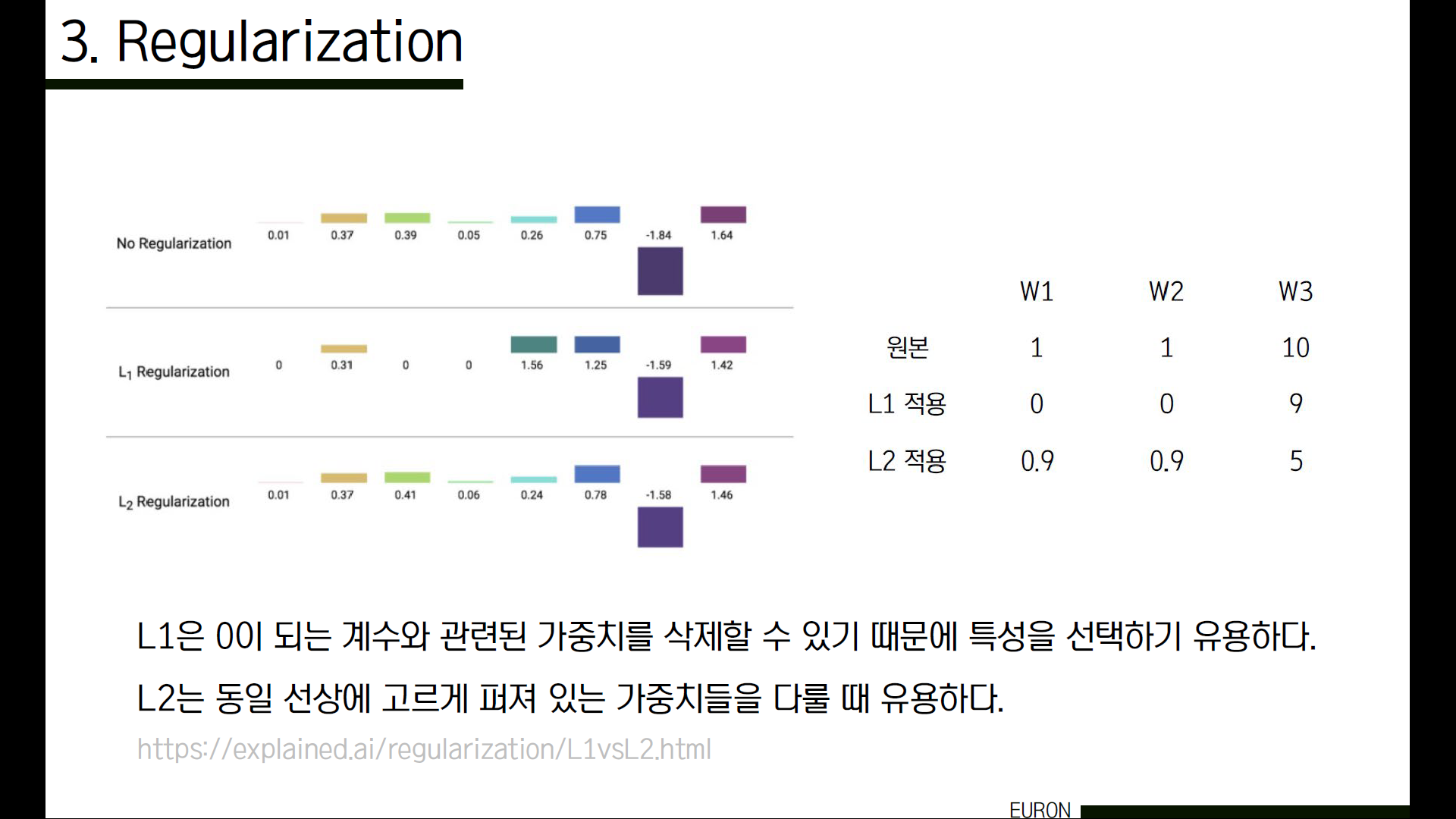
L1과 L2 규제를 사용해 정규화한 결과를 보겠습니다. L1에는 아주 작던 가중치들이 0으로 사라진 것을 확인할 수 있는 반면, L2 규제를 사용한 경우 아주 작더라도 남아있는 것을 볼 수 있습니다. 단, 이렇게 작은 가중치들은 큰 영향을 미치지는 못하겠죠.
예를 들어서 가중치 1,2,3이 각각 1,1,10이라고 해보겠습니다. L1 규제의 경우 모든 가중치에 대해 동일한 규제를 실시해 많은 ‘0’을 만들고자 하고, L2 규제의 경우 각각의 가중치를 고려해 규제를 적용하는 것을 볼 수 있습니다.
이처럼 L1은 0이 되는 계수와 관련된 가중치를 삭제하고 원하는 특성을 선택해 다루기 유용하고, L2는 모든 가중치를 고려해 최대한 고르게 규제를 적용하는 것을 볼 수 있습니다. 아래 링크는 L1과 L2 규제를 자세하게 비교한 내용을 찾아볼 수 있는 사이트입니다. 조금 더 자세하게 알아보고 싶으신 분은 참고하시면 좋을 것 같습니다.

이것도 같은 예시인데요. 보시다시피 L2는 각각의 벡터 값을 제곱해서 더한 후 루트를 씌우기 때문에 모든 벡터 값에 대해 항상 unique한 값을 내지만, L1 같은 경우에는 0과 같이 특정한 벡터의 요소 없이도 같은 값을 낼 수 있습니다. 해결하고자 하는 task에서 complexity가 어떻게 측정되어야 하는지에 따라 적절하게 정규화 방식을 선택해서 사용하면 됩니다.

즉 정규화는 training data에 정확하게 맞추는 것보다는 복잡한 모델에 대해 다소 패널티를 줌으로써 실제 test data를 예측할 수 있는 더 단순한 model을 만드는 방법입니다. 단순한 모델을 선호하는 것과 학습 데이터에 모델을 맞추는 것 사이에서 균형을 맞추기 위해 노력해야 합니다.
요약하자면, 모델에 사용될 함수 F를 지정하려고 할 때, 매개 변수 값에 따라 알고리즘이 얼마나 잘 작동하는지를 결정하는 loss function을 지정하고, 모델의 복잡함에 패널티를 주는 방법인 정규화 방법을 선택합니다. 그 다음 이 두 가지를 적절하게 조절하여 최종 loss function을 최소화하는 W를 찾습니다. 이 loss를 최소화하는 W를 찾는 방법인 optimization에 대해서는 다음 포스트에 이어 작성하겠습니다.
'Study > CS231n' 카테고리의 다른 글
| CS231n - Lecture 7 (Optimizer) (0) | 2021.06.06 |
|---|---|
| CS231n - Lecture 6 (Training Neural Networks I) (0) | 2021.05.14 |
| CS231n - Lecture 5 (ConvNet) (0) | 2021.05.09 |
| CS231n - Lecture 4 (Backpropagation) (0) | 2021.05.09 |
| CS231n - Lecture 2 (1) | 2021.03.30 |




댓글