CS231n Lecture6 - Training Neural Networks를 듣고 정리한 내용입니다. 오류를 발견하시면 댓글로 말씀해주세요.
(강의 노트와 강의 영상의 분량이 정확하게 일치하지 않아 내용이 겹치는 강의노트의 링크를 모두 첨부하고 있습니다.)
CS231n Convolutional Neural Networks for Visual Recognition
Table of Contents: Quick intro It is possible to introduce neural networks without appealing to brain analogies. In the section on linear classification we computed scores for different visual categories given the image using the formula \( s = W x \), whe
cs231n.github.io
CS231n Convolutional Neural Networks for Visual Recognition
Table of Contents: Setting up the data and the model In the previous section we introduced a model of a Neuron, which computes a dot product following a non-linearity, and Neural Networks that arrange neurons into layers. Together, these choices define the
cs231n.github.io
아래는 앞으로 Nerual Network와 관련해서 살펴볼 내용이다.


1. Activation Functions
neural networks는 input data를 비선형적인 activation function에 통과시켜 얻은 결과값을 다음 layer로 넘기기 때문에 어떤 activation function을 사용하는지에 따라서 학습 결과가 달라질 수 있다. 이번 시간에는 activation function에는 어떤 것들이 있는지 살펴볼 것이다.

(1) Sigmoid
시그모이드 함수는 전통적으로 많이 사용되는 함수인데 (이전 시간에도 많이 언급되었다.) 각 입력값들을 모두 0~1 사이의 값으로 바꿔 표현하는 비선형 구조이다. 이제는 시그모이드 함수를 잘 사용하지 않는데, 그 이유는 다음과 같다.
1. x값이 매우 크거나 매우 작을 경우 기울기가 모두 0이 된다. (Saturated neurons "kill" the gradients.)

그래프를 확인해보면 x = -10이거나 x = 10일 때 gradient가 0인 것을 볼 수 있다. 이것처럼 x가 매우 커지거나 매우 작아질수록 sigmoid 함숫값이 0 또는 1에 매우 가까워져 전체적으로 기울기가 x축에 평행해진다. 이를 saturated하다라고 표현하는데, 이 경우 backpropagation을 할 때 모두 0이 곱해지면서 학습이 더 이상 진행되지 않는 치명적인 문제를 발생시킨다.
2. 시그모이드 그래프의 중심이 0인 형태가 아니다. (Sigmoid outpus are not zero-centered.)
Zero-centered란 그래프의 중심이 0인 상태로, 함숫값이 음수 혹은 양수에만 치우쳐 존재하지 않고 실수 전체에서 고르게 나타나는 형태를 의미한다. 하지만 시그모이드는 위의 그래프에서도 볼 수 있듯이 함숫값이 항상 0~1이기 때문에 함숫값이 양수만 존재한다.

위의 예시를 통해 이것의 문제점을 알아보자. Neural networks에서 input은 예전 layer의 결과값이라고 생각하면 된다. (activation function을 통과한 결과 값을 다음 layer에 넘기기 때문) 그런데 시그모이드 함수의 결과값은 항상 양수이기 때문에 시그모이드 함수를 한번 거친 이후로는 이 input 값이 항상 양수가 된다. 이렇게 되면 backpropagation을 할 때 문제가 생긴다. backpropagation을 하게 되면 chain rule을 사용하는데, dL/dw = dL/df * df/dw 의 계산 과정을 거칠 때 df/dw = x이므로 dL/dw = dL/df * x가 된다. 이렇게 되면 input값인 x(local gradient)가 항상 양수이기 때문에 dL/dw와 dL/df의 부호는 같을 수밖에 없다.
w가 2차원이라고 하면 좌표 평면에서 부호를 따져봤을 때 부호가 같은 부분은 1,3사분면이다. 따라서 가상 최적 w는 파란색 벡터임에도 불구하고, 빨간색 벡터처럼 지그재그의 형태로 기울기가 업데이트(학습) 될 수밖에 없다. 그렇기 때문에 zero-centered가 필요하다. input x의 부호가 다양해야 기울기를 업데이트 할 때 적절한 방향으로 진행할 수 있기 때문이다.
3. exp() is a bit compute expensive
마지막으로 exp()계산은 상대적으로 계산이 힘들다.
(2) tanh(x)

zero-centered인 것은 좋으나, 역시 x값이 ∞나 -∞에 가까울수록 x축에 평행한 모습을 볼 수 있다. 즉, saturated할 때 gradient가 0이 된다는 단점이 있다.
(3) ReLU
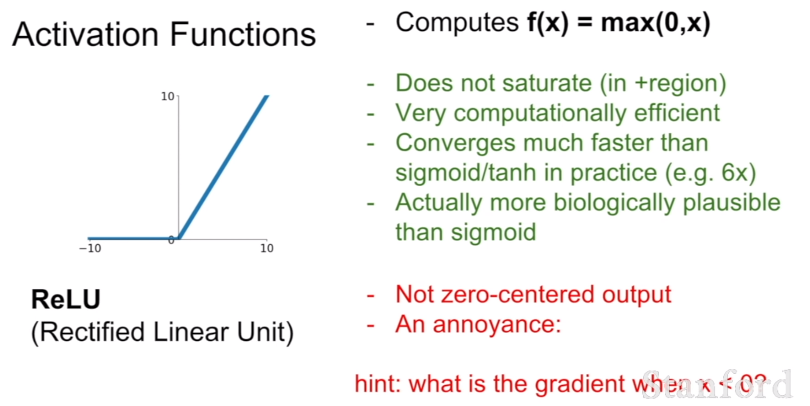
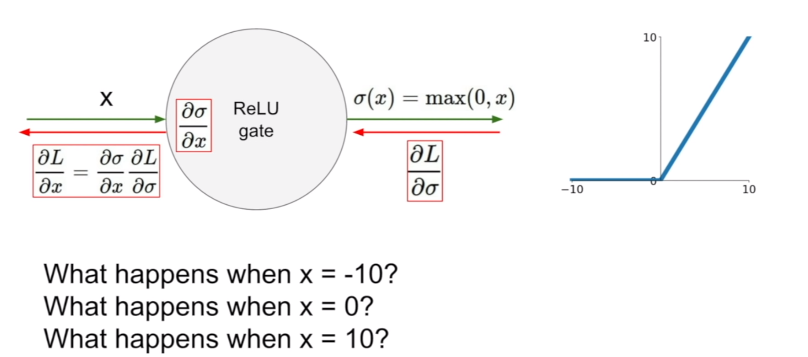
가장 많이 사용된느 함수는 ReLU다. x가 양수인 지점에서 gradient가 0이 되는 문제가 없으며, 단순히 max 함수를 사용하기 때문에 약 6배 정도 빠르다는 장점이 있다. 하지만 역시 함숫값이 모두 양수이기 때문에 output이 zero-centered하지 못하다는 단점이 있으며, 절반에 해당하는 부분(x가 음수인 부분)에서는 saturated하기 때문에 학습시 gradient를 0으로 만드는 문제가 있다.

또한 learning rate를 너무 크게 잡으면 data cloud 밖에서 actiavted되는 문제가 발생하는데, 이를 dead ReLU라고 부르며, 이러한 경우에는 다시 활성화되지 못해서 학습이 더 이상 진행되지 않는다는 치명적인 문제가 발생한다. 따라서 ReLU를 사용할 때는 learning rate를 작은 값으로 초기화하는 것이 필요하다.
=> people like to initialize ReLU neurons with slightly positive biases (e.g. 0.01)
(4) Leaky ReLU, PReLU

ReLU가 x가 음수인 부분에서 saturated 되는 문제를 해결한 함수이다.
(5) ELU

ReLU와 Leacky ReLU 사이에 해당하는 함수라고 이해하면 된다. ReLU의 장점을 모두 가지고 있으며(x가 양수일 때), 평균 출력이 0에 가깝고, Leaky ReLU와는 다르게 음수 부분에 saturation이 있어 노이즈에 대한 견고함(영향을 받지 않는 것)이 더해진 형태이다.
(6) Maxout

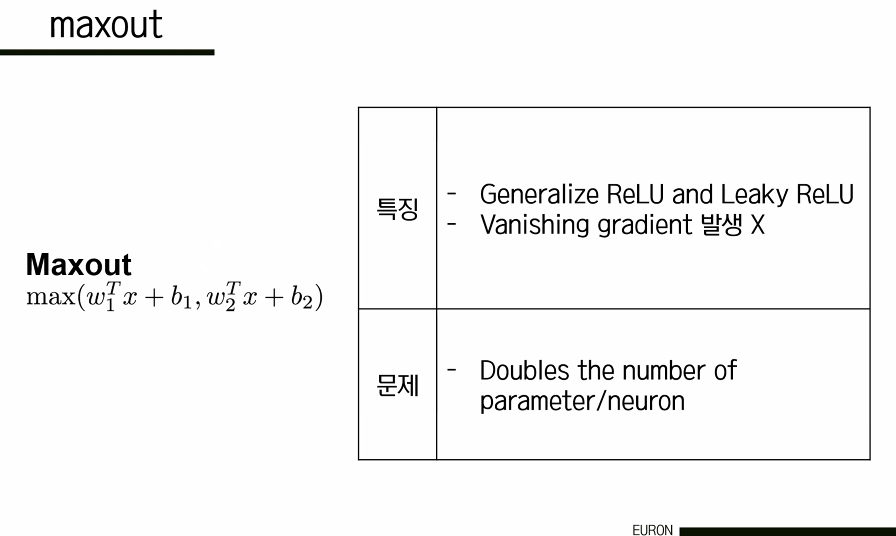
Maxout은 ReLU와 Leaky ReLu를 합쳐서 계산한 것으로 각각의 단점을 상쇄시킨다는 장점이 있지만 연산량이 두 배로 증가한다는 단점이 있다.


즉, 시그모이드 함수를 쓰지 말고 ReLU를 쓰되, learning rate를 신경써야 한다는 결론이다.
2. Data Processing
이미지 데이터 전처리 과정에서는 일반적으로 zero mean processing(zero-centered 처리)을 진행한다. 모든 특징들이 동일한 범위에 있도록 데이터를 정규화해서 그 특징들이 결과에 동등하게 기여할 수 있도록하는 것이다. training data에서 평균 이미지 채널 계산하고, 이것을 각 이미지 채널에서 빼는 방식이다.

Q) 이미지의 '채널'은 어떤 의미인가?
RGB. 이미지는 일반적으로 32x32x3이다. RGB에 해당하는 채널당 평균을 갖게 된다.
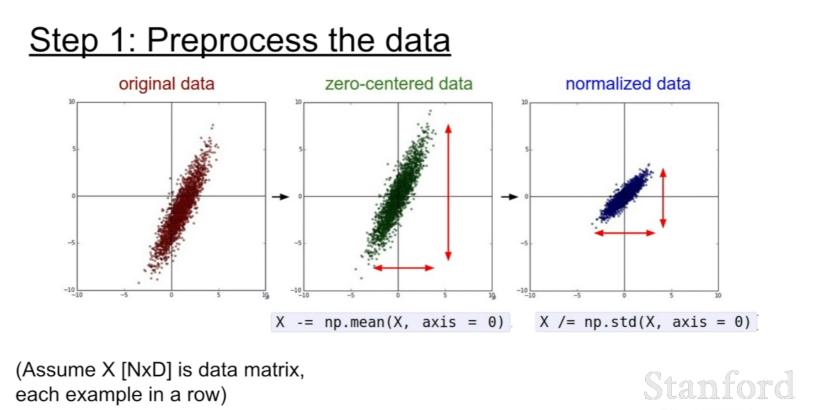
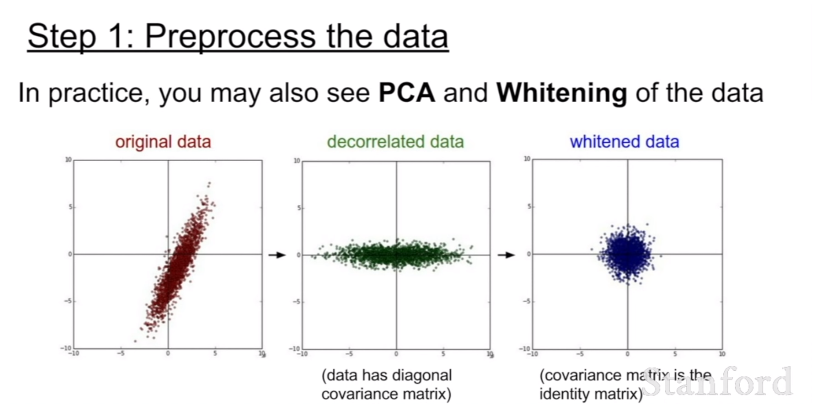
하지만 일반적으로 이미지의 경우에는 픽셀들을 너무 많이 정규화할 필요가 없다. 왜냐하면 이미지는 각 위치에서 이미 비교적 비슷한 규모와 분포(0~256)를 가지고 있기 때문이다. 따라서 zero-centering 정도만 해주면 충분하다. 우리는 전형적으로 convolutional networks를 공간적으로 적용해서, 원본 이미지 위에서 공간 정보를 포함한 형태로 특징을 추출해낸다.
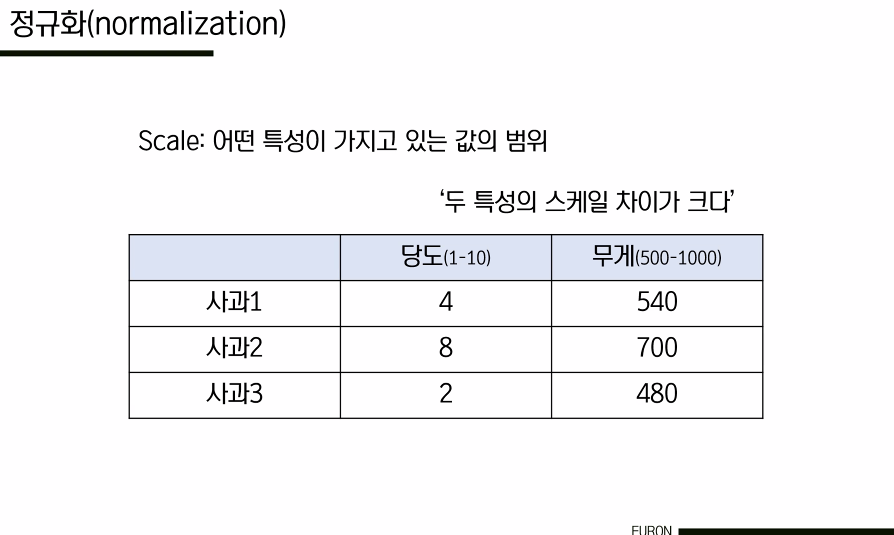

Q) 데이터 전처리 과정이 시그모이드의 문제점을 해결할 수 있지 않은가?
맞다. 첫 번째 레이어에 대해서는 이 문제를 해결할 수 있다. 하지만 우리는 깊은 네트워크를 갖고 있기 때문에 뒤로 갈수록 이것뿐만이 아니라 더 심각해진다. 따라서 이 경우에는 데이터 전처리 과정만으로 충분히 해결되지 않는다. 즉, 이것은 네트워크의 첫 번째 계층에서만 도움이 된다.
3. Weight Initialization

Q) 모든 parameter를 0으로 설정할 경우 어떻게 되나?
모든 뉴런은 같은 일을 한다. 가충치가 0이기 때문에 입력이 주어지면 모든 뉴런은 기본적으로 동일한 작업을 하게 된다. 즉, 같은 값을 출력할 것이기 때문에 동일한 gradient를 갖게 되고, 동일하게 학습된다. 우리는 뉴런이 다른 것을 학습하기를 바란다. 이것이 모든 것을 똑같이 초기화하면 안 되는 이유다.
(1) Small random numbers

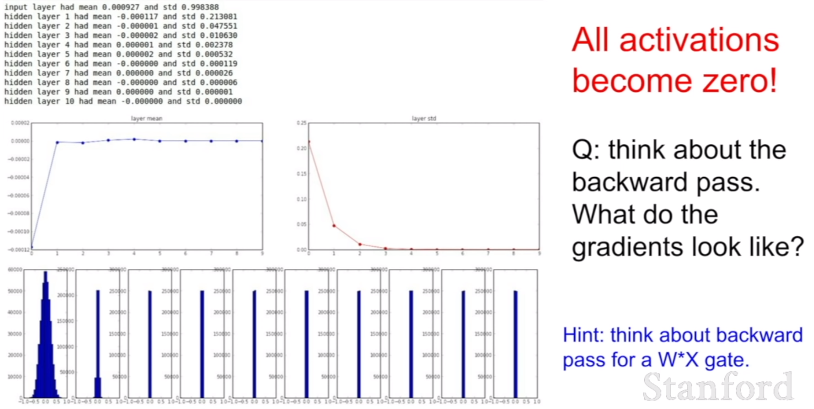
위의 문제를 해결하기 위한 첫 번째 방법은 모든 가중치를 아주 작은 난수로 초기화하는 것이다. 하지만이 방법은 간단한 네트워크에서는 괜찮겠지만 뉴런들이 복잡해질수록 모든 값이 0에 가까워지는 문제가 발생한다. 오른쪽 표를 보면 첫 번째 뉴런에서는 평균을 0으로 하고 적절한 표준편차를 갖고 있는 형태로 보이나, 뒤로 갈수록 점점 0이 되어가는 모습을 확인할 수 있다.
Q) 기울기는 어떻게 될까?
입력값이 매우 작다. weight에 대한 gradient는 upstream gradient * local gradient이다. 이 dot product는 W x X를 수행하는데, 기본적으로 X가 된다. 바로 입력값이다. 따라서 X가 작기 때문에 가충치는 매우 작은 기울기를 얻게 되고, 업데이트 되지 않는다.
(2) Large random numbers

표준편차 0.01대신 1을 사용한 예시다. 가중치가 커졌기 때문에 tanh를 통과한 값들이 saturated된다. 가중치가 커진다는 것은 항상 saturated 상태에 있다는 것이다. 가중치가 1 또는 -1이 된다. 즉, 너무 큰 값도 좋지 않다.
(3) Xavier Initialization
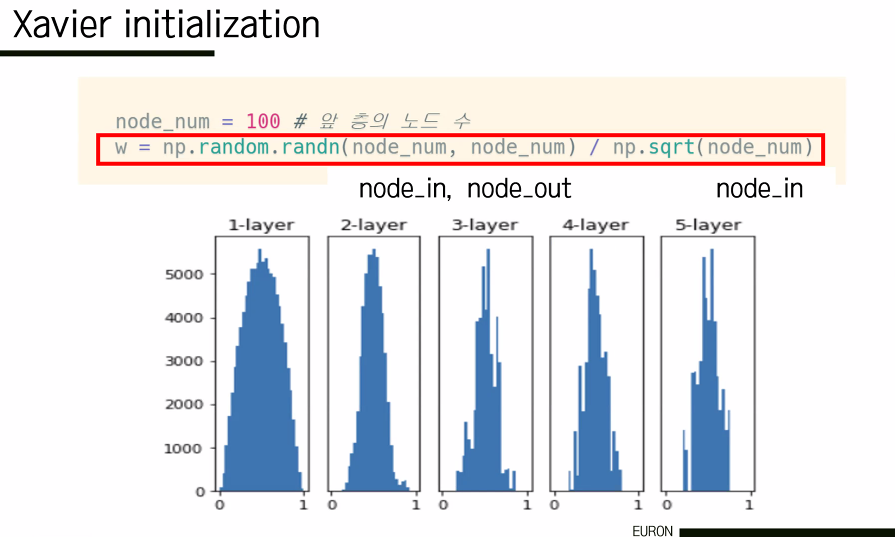
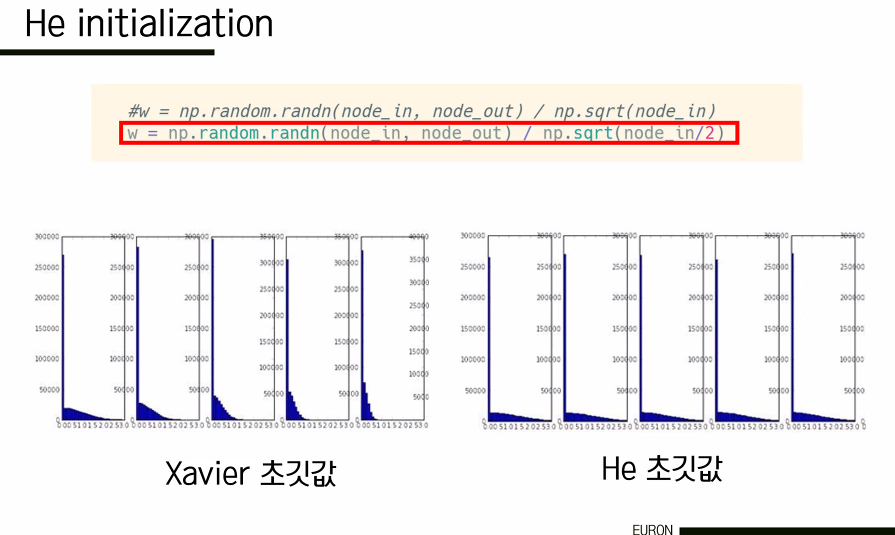
선형적인 case에는 적절하다. 이전 노드의 개수가 많아지면 weight 값이 작아지고, 반대면 커진다. 입력의 수에 따라 가중치의 크기가 달라지기 때문에 saturation이 발생하지 않고 고르게 분포하게 된다. 그러나 ReLU와 같은 비선형 case에는 적절하지 않은데, ReLU의 특성을 생각해보면 음수인 경우 모두 가중치가 0이었기 때문에 기울기도 반토막이 된다. 따라서 비선형 case에 대해서는 he 초기값을 사용한다.
4. Batch Normalization
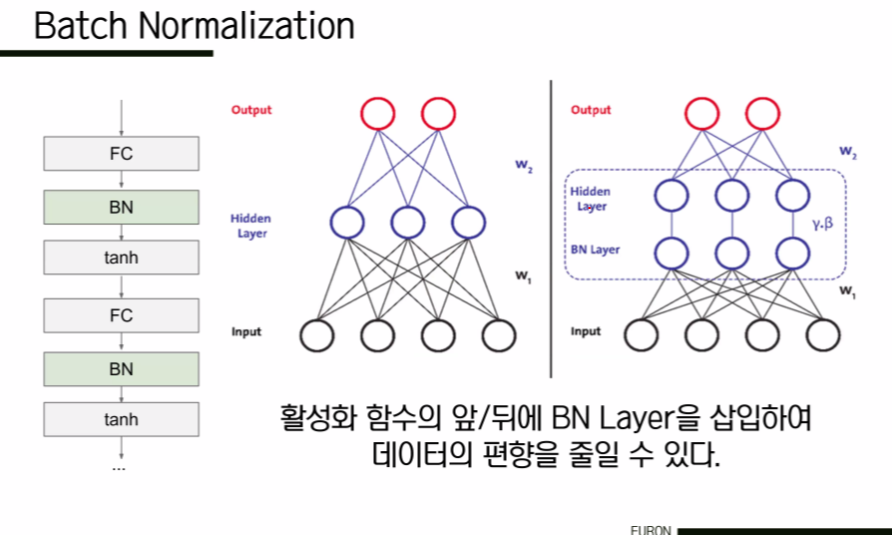

BN Layer는 일반적으로 FC 혹은 Conv layer 뒤와, non-linear func 전에 삽입된다. Mini Batch 단위로 정규화를 수행한다. 초기값을 설정하는데 많은 공을 들이지 않고도 활성화값 분포를 적당히 퍼트릴 수 있도록 강제할 수 있다는데 이점이 있다. 모델이 학습됨에 따라 감마와 베타도 학습될 수 있다. dropout의 필요성을 약간 감소시켜준다.
dropout이란? hidden layer의 임의의 레이어를 누락시키는 방법이다. 수행할 때마다 누락된 뉴런이 바뀌어서 다른 feature로 학습한 효과가 발생해 ensemble 효과와 유사한 효과를 거둘 수 있다. 이를 통해 하나의 특정 특징에 대한 편향을 방지하고, 다양한 특징이 골고루 이용될 수 있도록 해서 overfitting을 방지하는 기술이다.
Q) tanh layer에는 반드시 가우시안 단위의 입력이 필요한가?
"saturated를 어떻게 처리할 것인가"라는 점에서 그렇다. 정규화 후 네트워크는 학습을 통해 범위를 축소할 수 있다. 감마와 베타는 모두 매개변수(parameter)다. To be learned, gamma is scaling and beta is shifting. (BN just scaling and shifting. It does not change structure.) 이것들은 BN이 작동하는 방식에 유연성을 부여하는데 사용된다. 예시로, 학습 네트워크는 어떻게 saturated 될 것인지 방법을 선택할 수 있다.


Batch Normalization은 경험적인 평균 훈련 시간, 훈련 데이터의 분산 정도를 계산한다. 따라서 우리는 테스트 시간에 이것을 다시 계산하지 않고, 훈련 시간에 실행 평균 시간을 추정해 테스트 시간에 사용한다.
5. Babysitting the Learning Process

훈련 모니터링 방법에 대해 이야기할 차례다. 항상 그렇듯 우리가 가장 먼저 하고 싶은 것은 데이터를 전처리해서 데이터의 평균을 0으로 만드는 것이다. 그 이후 아키텍처를 정하고, 하나의 hidden layer에서 학습을 시작한다. 그 이후 가장 먼저 하고 싶은 것은 바로 네트워크를 초기화하는 것이다.

우리는 먼저 우리가 구한 loss가 합리적인지 확인해야 한다. 저번 강의에서 배운 Softmax를 사용한다고 해보자. w가 매우 작으면 결과값인 loss는 -log의 형태이므로 (loss가 정확히 구해지고 있다면) 결국 우리가 기대하는 0이라는 값이 나올 것이다. 그래서 이것은 좋은 sanity check 방법이 되는 것이다. 이렇게 우리의 loss가 잘 나온다는 것을 확인할 수 있다.

we want to crank up the regularization. 추가적으로 정규화를 진행했기 때문에 loss가 증가하는 것을 확인하고 싶다. 그리고 원하던대로 loss가 증가한 것을 확인했다. 그렇다면 loss가 좋다는 것이 확인되었기 때문에 다음 단계로 넘어가보자.

이 과정에서 정규화를 제외하고 loss를 0으로 낮출 수 있는지 다시 확인한다. 현재 훈련 데이터의 양이 적기 때문에 훈련 정확도를 1에(overfit) 맞출 필요가 있다.
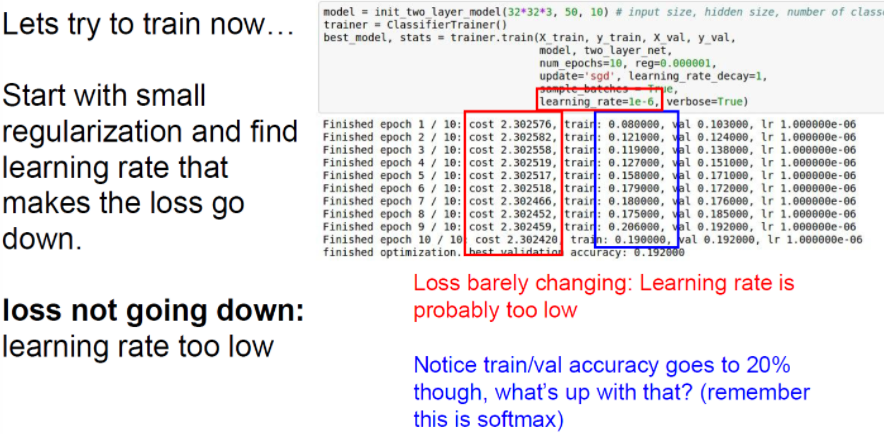

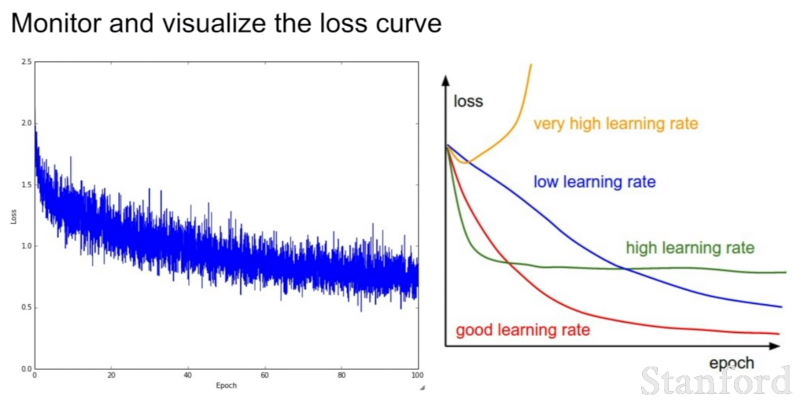
learning rate가 너무 작으면 loss가 거의 변하지 않는다. 따라서 learning rate가 너무 작으면 gradient update가 충분히 크지 않다. cost는 기본적으로 거의 같다. 반대로 learning rate가 매우 크면 어떻게 될까? cost가 NaN으로 나온다. 비용이 매우 크다는 뜻이다.

따라서 다시 학습률을 낮추며 확인해보자. 결과적으로 1e-3과 1e-5 사이가 우리가 원하는 대략적인 범위이다. 이 범위 안에서 learning rate를 조절하면 된다.
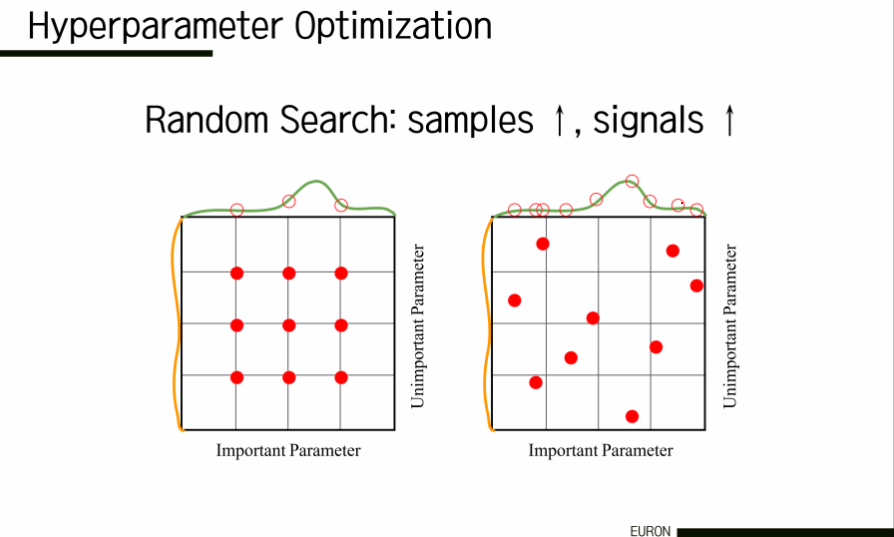
6. Hyperparameter Optimization
그렇다면 이러한 learning rate와 같은 hyperparmeter 중 어떻게 가장 좋은 값을 선택하는가? hyperparameter를 정하는 대표적인 방법 중 하나는, 예전에 다뤘던 교차 검증(cross-validation)이 있다. 교차 검증은 다시 말해서 훈련 세트에 대한 훈련이다.

'Study > CS231n' 카테고리의 다른 글
| CS231n - Lecture 7 (Regularization) (0) | 2021.06.08 |
|---|---|
| CS231n - Lecture 7 (Optimizer) (0) | 2021.06.06 |
| CS231n - Lecture 5 (ConvNet) (0) | 2021.05.09 |
| CS231n - Lecture 4 (Backpropagation) (0) | 2021.05.09 |
| CS231n - Lecture 3 (Loss Functions) (3) | 2021.04.08 |




댓글