CS231n Lecture5 - Convolutional Neural Networks을 듣고 정리한 내용입니다. 오류를 발견하시면 댓글로 말씀해주세요.
CS231n Convolutional Neural Networks for Visual Recognition
Table of Contents: Convolutional Neural Networks (CNNs / ConvNets) Convolutional Neural Networks are very similar to ordinary Neural Networks from the previous chapter: they are made up of neurons that have learnable weights and biases. Each neuron receive
cs231n.github.io
1. ConvNet (CNN/Convolutional Neural Networks)

ConvNet은 여러 레이어로 이루어져 있다. 각각의 레이어는 3차원의 볼륨을 입력으로 받고 미분 가능한 함수를 거쳐 3차원의 볼륨을 출력하는 기능을 한다. ConvNet의 각 레이어는 미분 가능한 변환 함수를 통해 하나의 activation volume을 또 다른 activation volume으로 변환시킨다. ConvNet 아키텍쳐에서는 크게 convolutional layer, pooling layer, fully-connected layer라는 3개의 레이어가 사용된다. 이 전체적인 과정을 크게 세 부분으로 나눠서 기능을 설명해보자면 아래와 같다.
* input layer : 이미지를 입력
* Conv ~ Pool : 이미지의 특징을 뽑아내고 차원을 낮추는 과정(depth는 유지됨)
* FC : 결과를 점수화시켜 어떤 분류에 해당하는 이미지인지 결정하는 과정
ConvNet은 우리가 이전까지 살펴봤던 일반 신경망과 매우 유사하다. 학습 가능한 가중치(weight)와 편향(bias)으로 구성되어 있으며, 각 뉴런은 입력을 받아 내적 연산(dot product)을 한 뒤, 선택에 따라 non-linear 연산을 한다. 전체 네트워크는 일반 신경망과 마찬가지로 미분 가능한 하나의 score function을 갖게 된다. 마지막 레이어에 loss function을 가지며, 우리가 일반 신경망을 학습시킬 때 사용하던 각종 기법들을 동일하게 적용할 수 있다. ConvNet 구조를 사용할 경우 forward function을 더욱 효과적으로 구현할 수 있고, 네트워크를 학습시키는데 필요한 parameter의 수를 크게 줄일 수 있다.
2. Convolution Layer


기존에는 왼쪽 이미지와 같이 input image를 길게 늘여서 계산했기 때문에 공간 정보가 유지되지 않았으며 이렇게 계산된 값은 하나의 특징만을 나타내게 되었다. (공간 정보를 포함하지 못한다.)
하지만 CNN은 공간 정보를 포함한다. 어떻게 된 걸까?
이미지보다 작은 filter(weight이다. 가중치를 주는 거라고 이해하면 된다.)를 정의한 뒤, 이미지의 왼쪽 위부터 오른쪽으로 dot product를 진행한다. dot product란, filter에 해당하는 부분에서 하나의 특징이 되는 값을 뽑아내는 계산 과정을 의미한다. 이렇게 dot product를 통해 나온 하나의 값은 activation map의 하나의 값을 구성한다. 이러한 방식으로 이미지의 모든 구역을 훑고 난 뒤 생성된 activation map은 각 공간에 대한 특징값들의 모임으로 생각하면 된다. 따라서 이미지 전체의 특징을 추출하는 것이 아닌 공간별 특징을 추출하여 표현하기 때문에 공간 정보를 유지한다고 하는 것이다.
이때, filter의 depth는 image의 depth와 동일하다. 이 dot product를 진행할 때, filter를 어떤 간격(가로/세로의 공간적 간격)으로 움직일지를 의미하는 stride를 결정해야 한다. 즉, filter가 합성곱을 진행할 때 '몇 칸씩 움직일 지'에 해당하는 값이 stride다. 자세한 dot product 계산 방법을 알아보기 전에, stride를 먼저 살펴보고 가자.



stride 값이 1인 경우이다. stride만큼 필터가 칸을 옮겨가며 합성곱이 진행되는 것을 볼 수 있다. 참고로 주로 Conv Layer에는 stride 1을 사용하는데, 보통 작은 stride가 더 잘 동작할 뿐만 아니라 모든 spatial downsampling을 Pool layer에 맡기게 되고 Conv Layer는 입력 볼륨의 깊이만 변화시키게 된다. 즉, 역할을 뚜렷하게 구분하기 위해서라고 할 수 있다.

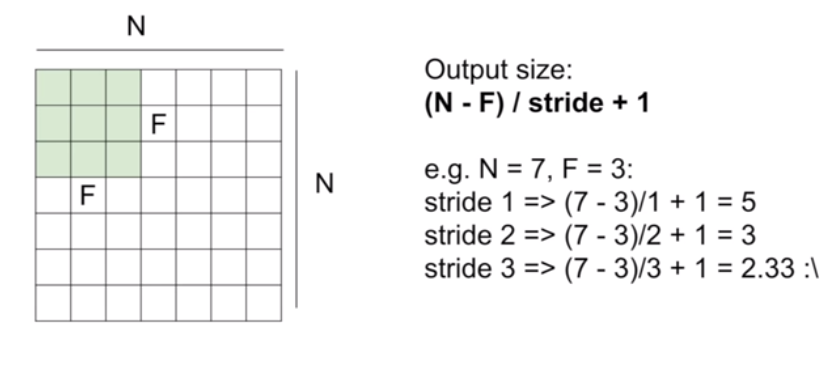
이렇게 stride에 따라 output size는 오른쪽의 공식에 따라 계산할 수 있다. stride 값이 커질수록 output size는 작아진다. 사실 당연한 말이다. filter를 통해 계산한 값인 activation map의 크기가 작아질 수밖에 없기 때문이다.
그렇다면 dot product의 합성곱은 어떻게 하는 건지 그 방법을 살펴보자.

input image의 값과 filter 값을 각각 곱해 더한 값이 output으로 activation map에 기록된다. 위의 그림을 예시로 들자면, (2x1) + (3x0) + (4x1) + (1x1) + (0x0) + (1x1) + (0x0) + (1x1) + (1x0) = 9 이다. 이렇게 모든 input image에 대해서 filter로 dot product를 진행하면 activation map을 채울 수 있다.
그런데 이제 filter의 크기가 커지면 activation map의 크기는 빠르게 작아진다. 또한, layer를 많이 사용하지 못하게 된다. 이 방법을 해결하기 위해 padding이라는 것이 존재한다.


기존 방법대로 합성곱을 실행할 경우, output size가 input size보다 작아지는 문제가 발생한다. 이를 방지하기 위해서 input image를 0으로 둘러싼 뒤에 합성곱을 진행하게 되는데, 이것을 패딩이라고 한다. 만약 잘 이해가 되지 않는다면 위의 예시에 테두리를 0으로 채운 후 합성곱을 진행해보자. output size가 input size와 동일하게 나오는 것을 확인할 수 있다. 물론 공식으로도 output size를 구해볼 수 있다. stride가 1일 때, (N-F+2P)/stride +1에 수를 대입해 계산해보면, input size와 동일한 값이 나온다는 것을 알 수 있다.
Conv Layer를 통과하면서 spatial 크기를 그대로 유지하게 해준다는 점 이외에도, 패딩을 쓰면 성능도 향상된다. 만약 제로 패딩을 하지 않고 valid convolution을 한다면 볼륨의 크기는 Conv Layer를 거칠 때마다 줄어들게 되고, 가장자리의 정보들이 빠르게 사라지게 될 것이다.
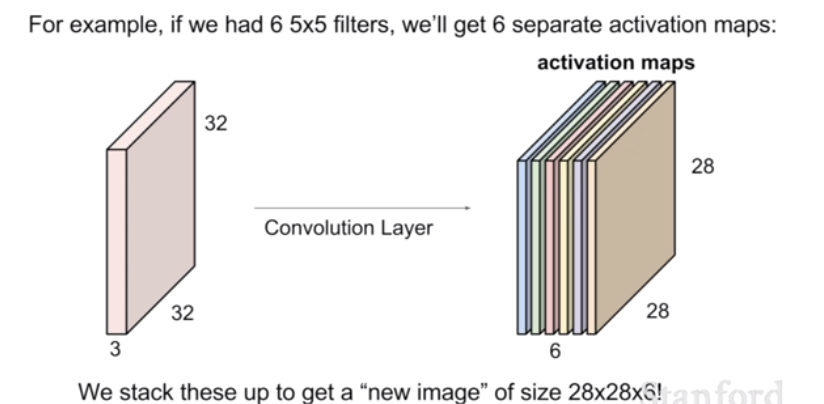

만약 filter를 여러 개 사용하게 된다면 filter의 개수만큼 activation map이 형성될 것이다. 이렇게 Conv layer를 쌓아나가면서 CNN을 완성시킨다. 그렇다면 아래의 문제를 풀어보자.
Q) 다음과 같은 조건일 때 output activation map의 size를 구하시오.
input volume : 32x32x3
7x7 filter (stride : 1) 4개 사용
(N-F) / stride + 1 의 공식에 따라 (32-7)/1 +1 = 26이기 때문에 activation map 1개의 size는 26이다. 그런데 filter 4개를 사용했다고 했으므로 답은 26x26x4가 될 것이다. 아래의 예시를 보며 output volume size와 parameter의 개수를 구하는 방법에 익숙해져보자.
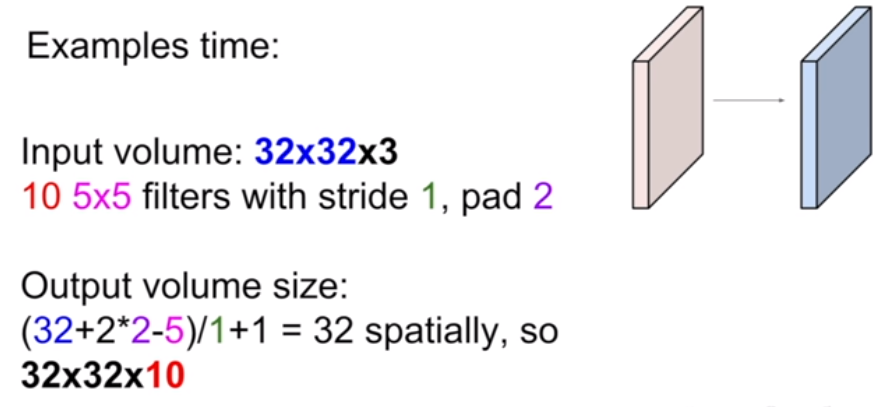

3. Pooling Layer
위에서 소개했듯이, CNN은 Conv layer, RELU, Pooling layer가 한 세트로 이루어져 있으며, 이것들을 차례로 쌓은 후, 마지막을 fully-connected layer로 구성한다. pooling layer는 spatial 차원에 대한 downsampling을 위해 사용된다. 추출한 특징을 최대한 유지한 채 이미지의 크기를 줄여주는 장치이다.
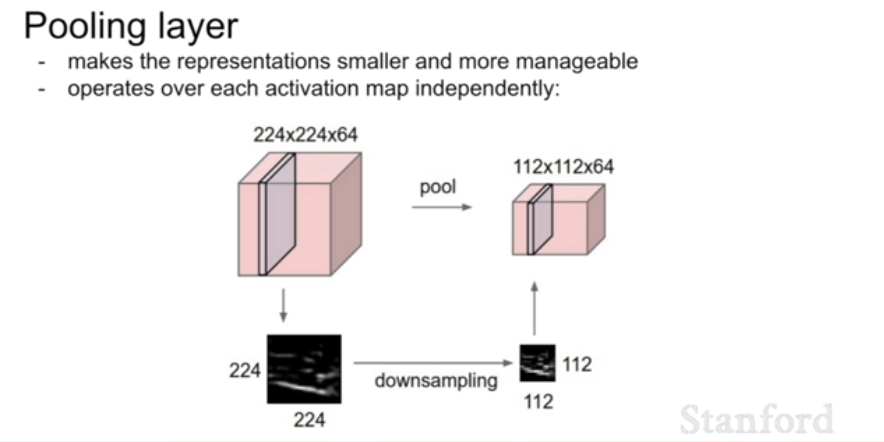
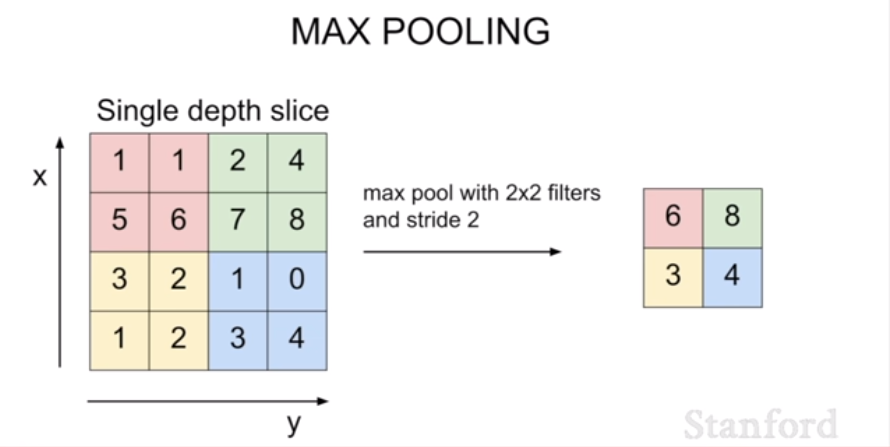
가장 많이 사용되는 방식은 Max Pooling 방식이다. (별다른 언급이 없다면 Max Pool이라고 가정한다.) Pooling layer에서 사용할 filter의 크기와 stride 값을 정한 뒤 filter가 합성될 때 이전처럼 dot product를 진행하는 것이 아니라 max 값만 산출하는 것이다. 이렇게 하면 가장 큰 특징을 살리면서 이미지의 크기를 줄여나갈 수 있다. pooling layer는 주로 2~3번 거치는 것이 가장 이상적이다.
이후 fully-connected layer에 넣어 각 class 별로 예측치를 산출하면 CNN이 완성된다. fully-connected 레이어 내의 뉴런들은 일반 신경망 챕터에서 보았듯이 이전 레이어의 모든 activation들과 연결되어 있다. 그러므로 fully-connected 레이어의 액티베이션은 합성곱을 한 뒤 bias를 더해 구할 수 있다.


'Study > CS231n' 카테고리의 다른 글
| CS231n - Lecture 7 (Optimizer) (0) | 2021.06.06 |
|---|---|
| CS231n - Lecture 6 (Training Neural Networks I) (0) | 2021.05.14 |
| CS231n - Lecture 4 (Backpropagation) (0) | 2021.05.09 |
| CS231n - Lecture 3 (Loss Functions) (3) | 2021.04.08 |
| CS231n - Lecture 2 (1) | 2021.03.30 |




댓글